2017-10-03

文体のパターンの繰返しで深層学習する論文を読む

AI論文自然言語解析

ランニングできず英語できず

(1) 文体のパターンの繰返しで深層学習する論文を読む

「Dynamic Evaluation of Neural Sequence Models」 https://arxiv.org/abs/1709.07432

一般に自然言語の深層学習では単語間の繋がりをLSTMで学習することが殆どですが、近年構文を学習するHocherのモデルや意味データベースを使って解析を強化するモデルも出現してきています。

この論文は長文の構造が似た文体が繰返し出現することに注目し、文体を表す隠れ変数 $\theta_l$ で生成される文が連結して構成されるとして解釈するモデルです。

　このモデルをdynamic evalと称しています。

　文体を表す隠れ変数 $\theta_l$ を仮定すると文章の尤度は次式となります。

　　 $P(x|\theta_g) = \Pi_{k=1}^N P(s_k| \theta_l^k) \cdot P(\theta_l^k)$

$x = \{s_1,s_2,\dots,s_N \}$

ここで

　　　 $x$ ：文章全体

$s_k$ ：文 or 固定長の文字列

$\theta_l$ ：文体を表す隠れ変数

$\theta_g$ ：文章全体を表す隠れ変数

　このモデルでは下図の様にRMSprop型を修正した深層モデルで

隠れ変数 $\theta_l^k \ \theta_g$ を解いています。

　この論文では明記されていませんが下図のmodel(si,θi)はLSTMと解釈されます。

f:id:mabonki0725:20171004002831p:plain

(1.1)手法

　自然言語の深層学習にはRNNやLSTMを使うのが一般的ですが、文体間の生成モデルなので深層学習のパラメータ更新タイプのRMSpropの更新規則を改修し使っています。

　このパラメータの調整は一般のニューロモデルと同じです。最終的に生成した文章と実際の文章の相違より逆伝播してパラメータを調整しています。

　但しパラメータの更新規則はRMSpropの修正版を使っています。

　RMSpropの更新規則は以下です。

　 $h_{t} = \alpha h_{t−１} + (1 - \alpha) \nabla E(\mathbf{w}^{t})^{2}$

　 $\eta_{t} = \frac{\eta_{0}}{\sqrt{h_{t}} + \epsilon}$

　 $\mathbf{w}^{t+1} = \mathbf{w}^{t} - \eta_{t} \nabla E(\mathbf{w}^{t})$

　このRMSpropを以下に置き換えしています。

　　　 $h_{t-1} \to MS_{t-1}$

　 $\nabla E(\mathbf{w}^t)^2 \to (\nabla \theta_l^t)^2$

　また文体の連鎖を計算するため以下を計算します。

　　　 $\mathcal{L}(s_t)$ ： $\theta_l^t$ の生成規則で生成した文と実際の文 $s_t$ との相違による損失量

　ここからRMSpropの各項を計算します。

　 $\nabla \theta_l^t = \frac{\partial \mathcal{L}(s_t)}{\partial \theta_l^t}$

　　 $MS_t = (\nabla \theta_i^t)^2$

よって上記の置き換えを適用すると

$MS_t = \alpha MS_{t-1} + (1 - \alpha) (\nabla \theta_l^t)^2$

　　 $\eta_t = \frac{\eta_{0}}{\sqrt{MS_{t}} + \epsilon}$

$\theta_l^t \leftarrow \theta_l^{t-1} - \eta_t \nabla \theta_l^{t-1}$

　各 $\theta_l$ は文章全体の隠れ変数 $\theta_g$ に収束する必要があるので、

　上式のRMSpropの更新規則に正則化項としてこの制限を追加しています。

　　　 $\theta_l^t \leftarrow \theta_l^{t-1} - \eta \frac{\nabla \theta_l^{t-1}}{\sqrt{MS_g}+\epsilon} + \lambda(\theta_g - \theta_l^{i-1}) \cdot RMS_{norm}$

ここで

$RMS_{norm} = \frac{\sqrt{MS_g}}{avg(\sqrt{MS_g})}$

$MS_g= \frac{1}{N} \sum_{k=1}^N (\nabla \theta_l^k)^2$

(1.2) 結果

　Penn Treebank の文章でのPerplexityは以下の結果となっています。

Perplexityは文の複雑性を表し少ない程よいとされています。　

f:id:mabonki0725:20171003223428p:plain

ここで LSTM + dynamic evalとあるのは下図の構成になっているからです。

「Generating sequence withe recurrent neural networks」Graves (2013) より

f:id:mabonki0725:20171004072755p:plain

(1.3) 感想

　・ $\theta_g$ の更新規則は記述に無い様です。この辺は読み落としかもしれません。

　・簡単なロジックなので実装は容易かもしれませんが、LSTMの調整が難しそうです。

2017-10-02

強化学習方程式の不確実性を報酬に取込む論文を読む

ロボテックス AI論文

テニス２時間　英語できず

(1) 強化学習方程式の不確実性を報酬に取込む論文を読む

　「The Uncertaintry Bellman Equation and Exploration」

https://arxiv.org/abs/1709.05380

　この論文は強化学習を解くBellman方程式の近似解での不確実性を見積りより精緻に方程式を解き、既存のDQNを改善するものです。

　モデル名UBE(Uncertaintry Bellman Equaiton)

　一般に強化学習は将来の累計報酬の期待値が最大になる様に局面毎の行動を選択するモデルです。

　これはBellman方程式で行動価値関数として定式化されますが、将来への漸化式で解くので行動によって無限に分岐が続く場合、近似解で解くことが一般的です。

　 $Q^\pi(s,a) = \mathbb{E}\left(\sum_{t=0}^\infty \gamma^t r_t |s_0=s, a_0=a,\pi \right)$

ここで

$\pi$ は方策(policy)

　　　 $\gamma$ は割引率

$r$ は報酬

$s$ は局面

$a \sim \pi$ は行動で方策によって確率的に決定されます

また現報酬 $r(s,a)$ とそれ以降の行動価値関数 $Q^\pi(s',a')$ の和を行動価値関数 $T^\pi Q^\pi (s,a)$ であらわすと。

　　 $T^\pi Q^\pi(s,a) = \mathbb{E}_r r(s,a) + \gamma \mathbb{E}_{s',a'}Q^\pi(s',a')$

但し　 $s' \sim p(\cdot|s,a)$

(1.1) 手法

　一般に何らかなの霍乱要因 $d$ があると行動価値関数 $\hat{Q}(s,a)$ と推定された行動価値関数 $T^\pi Q^\pi (s,a)$ に差が出てきます。

　この差 $\epsilon(s,a)$ には認識できない報酬が存在しているからと考えられます。

　　 $\epsilon(s,a) = (\hat{Q}^\pi - T^\pi {Q}^\pi)(s,a)$

$= \hat{Q}^\pi(s,a) - \mathbb{E}_r r(s,a) - \gamma\mathbb{E}_{s',a'} Q^\pi(s',a')$

ここで $\delta(s,a) = \hat{Q}^\pi(s,a) - Q^\pi(s,a)$ を行動価値関数の差とすると

$\delta(s,a) = \epsilon(s,a) + \gamma \mathbb{E}_{s',a'} \delta(s',a')$

この二乗平均誤差は解析的に次式で表現できます

　 $m(s,a) = \mathbb{E}_d \left( (\hat{Q}^\pi(s,a) - Q^\pi(s,a))^2 \right)$

$= var \hat{Q}^\pi(s,a) + (biasQ^\pi(s,a))^2$

この霍乱要因 $d$ による行動価値関数の差はMarcovの不等式を使うと

　　 $Prob \left(|\hat{Q}^\pi(s,a) - Q^\pi(s,a)| \ge \alpha \cdot \sqrt{m(s,a)} \right) \le \frac{2}{\alpha^2}$

霍乱要因 $d$ の上式の下限を隠れた報酬 $u^*(s,a)$ として定理１を導入しています。

[定理1]

$u^*(s,a) = (T_u^\pi u^*)(s,a) = \beta^* var \epsilon(s,a) + \gamma^2 \mathbb{E}_{s',a'} u^*(s',a')$

この論文は隠れた報酬 $u^*(s,a)$ をDQNに与えてモデルを改善しています。

(1.2) 結果

　全ATARIゲームのDQNのスコアの中央値と不確定部分を隠された報酬とするUBEスコアの中央値との比較を示しています。

　ここで

instrinsic Motivation：擬似カウント

　　UBE n-step：隠れ報酬をn回刻みで計算する

f:id:mabonki0725:20171002234839p:plain

　「Montezumaの復習」は既存のDQNでは殆ど解けないモデルです。これには画面遷移を擬似カウントとして報酬とすると旨く行くことが知られています。UBEのスコアが上回っていますが、これは擬似カウントがUBEに反映されているからです。

　　 f:id:mabonki0725:20171002234918p:plain

2017-10-01

中国人達の深層Treeモデルの論文を読む

確率・統計

ランニングできず　英語できず

(1) 中国人達の深層Treeモデルの論文を読む

　「Deep Forest: Towards an Alternative to Deep Neural Networks」

https://arxiv.org/abs/1702.08835

　これは下図にある様にランダムフォレストを単に多層化したアンサンブル型モデルなので残念ながら理論的な新しさはありません。モデル名称はgcForest(Multi-Graind Cascade Forest)

　ランダムフォレスト自体がアンサンブル型なので深層にする意味が明確でないので構造が似ているDeepLearningと比較しています。　

　新興の中国人達がオリジナルな理論を構築できるまでは時間がかかりそうです。　

　そもそもアンサンブル型の優位性はJ.Friedmanが2000年に理論的に解明しました。

　またFriedmanはアンサンブル・ツリー＋ブースティング＋クロス・バリエーションとして各々の短所を補うモデルを提唱していて、これが現在Xgbootとなっています。

　DeepLearningは深層過程に於いて逆伝播して各層が独自の役割のフィルターを形成するもので、構造が似ているからと言って比較対象するものでは無いと思います。

　同じアンサンブル型であればXgboostと性能比較すべきと思います。

(1,1) 手法

f:id:mabonki0725:20171001230553p:plain

　このモデルは４個のランダムフォレストの深層モデルとなっていて、識別結果に入力データを再追加して次層に渡して深層化しています。

　（４個の内　2個は完全なランダムフォレスト　他の2個は入力データをランダムに短くしたランダムフォレストです）

　多分このモデルだと過学習の可能性があるので、各層毎にクロス・バリデーションをしています。

　最後にアンサンブルで識別結果を単純平均化しています。ランダムフォレストと同様にモデルの精度が頭打ちになると深層化を停止しています。

(1.2) 結果　

　結構面白いのは、DeepLeanningと対抗して文章の感情分析と画像識別をしていることです。　

f:id:mabonki0725:20171001234145p:plain

　結果はこの記述を信じれば意外に良好です　　　

　　 f:id:mabonki0725:20171001234349p:plain

顔の認識　　

　　 f:id:mabonki0725:20171001235052p:plain

　音楽の感情分析　

　　 f:id:mabonki0725:20171001234600p:plain

(1.3) 感想　

　アンサンブル型なのでXgboostでも同じ様に文章や画像の分析をしてみたら面白いと考えます。　　

2017-09-30

3D動画よりDoll House画像を生成する論文を読む

AI論文画像認識

ランニング30分　英語できず

(1) 3D動画よりDoll House画像を生成する論文を読む

「MatterPort3D: Learning from RGB-D Data in Indoor Environments」

https://arxiv.org/abs/1709.06158

　この論文は屋内をMatterPort3Dと云う動画で撮ると、深層学習により屋内をDollhouseの様に見せることができるものです。

f:id:mabonki0725:20171001002417p:plain

Mattterport3DカメラはMatterport社 https://matterport.com/ が販売するものです。

1) Matterport3Dデータの特性

　　このデータは次の様な優れた機能を有しています。

　・RGB-D Panorama

　　1280x1024 Colorの解像度で奥行きのデータもあります。

　　360度のパノラマ動画を録画します。　　　 f:id:mabonki0725:20171001000257p:plain

　・Precise Global Alignment

3D認識で1cm未満の精度があります。　　

　　　 f:id:mabonki0725:20170930231141p:plain

　　ここで

　　　奥行認識は観測点から大量の粒子を吹き付けた画像です

　　　法面表示は観測点からの面の向きによって色調を変えた画像です

　・Comprehensive Viewpoint Sampling

パノラマ動画用に2m置き程度にView Point(緑点)のデータを生成します。

　 f:id:mabonki0725:20170930231815p:plain

・Entire Buildings

90件の家の全階・全部屋の3D動画が可能

2)Matterport3Dのデータを深層学習を使って様々な認識を可能にしています。

　・フロアの識別

f:id:mabonki0725:20170930232442p:plain

　・物体の認識と種類の識別　　

　　　 f:id:mabonki0725:20170930232654p:plain

　3)深層学習による認識の方法

　　・教師用データの作成

　　　この様な認識をするため実際の画像から教師用ラベルを作成する必要があります。

　　　教師用のデータは「Amazon Mechanical Turk(AMT)」でツールと人力で構築しています。

　　　50811物体から1659のラベル付けをしています。

　　　言葉の意味階層モデルWordNetを使って最終的に40に絞っています。

f:id:mabonki0725:20171001095340p:plain

　　・画像認識　KeyPoint Matching

　　　異なるView Pointでの同じ物体の認識のため

　　　下図の３画像（一致用と非一致用）の教師データで訓練しています。

　　　特徴量は512個使用　ResNet-50での深層学習　　　

　　　 f:id:mabonki0725:20170930235055p:plain

　　・ View Overlap Prediction

　　　動画で同じ場面である認識をSLAMの仕掛けを利用しています。　

　　　画像 $A$ と $B$ の同じ場面かの識別は次式で行っています。

　　　　 $\mathcal{overlap}(A,B) = \frac{min(\hat{A},\hat{B})}{|A|+|B|-min(\hat{A},\hat{B})}$ 　

　　　　ここで

　　　　　 $|A|$ は奥行きが確かなpixel数

　　　　　 $\hat{A}$ は実際に5cm内の範囲で $B$ と重なっているpixelの数　

　　　 f:id:mabonki0725:20170930235424p:plain

　　　　　　　　写真の下段の数字は同じ場面の確率を示す

　　・法面認識　

　　　Matterport3Dデータは位置と奥行きのデータを持っているので容易に認識できます。

　　　この認識にはCNNを使っています。　　

　　　 f:id:mabonki0725:20170930235613p:plain

　　・局面の識別

　　　この局面認識ではCrowd-sourcingで構築した教師データを使って訓練しています。　　　

　　　 f:id:mabonki0725:20171001000006p:plain

　　・立体の認識

Metterport3Dデータを1.5m x 1.5m x 3m の長方体で切り出して、

　　　2cm刻みに小さくしていきます。これと教師データが70%以上一致すれば

　　　教師データと同じとしています。教師データは418840個あり、ScanNetで

　　　識別しています。

　　 f:id:mabonki0725:20170930235704p:plain

2017-09-29

PRMLのカルマンフィルターの変換行列の学習を理解する

確率・統計

ランニングできず　英語できず

(1) PRMLのカルマンフィルターの変換行列の学習を理解する

　「PRML 13§ 13.3.2 Learing in LDS」

カルマンフィルターの状態方程式はシステムモデルと観測モデルに分離して表現されます。

f:id:mabonki0725:20170926203958p:plain

　システム・モデル

　　　　 $p(z_n|z_{n-1},A,\Gamma) = \mathcal{N}(A\mu_{n-1},P_{n-1})$

$p(z_{n-1}) = \mathcal{N}(\mu_{n-1},V_{n-1})$

但し $P_{n-1} =A V_{n-1}A^T + \Gamma$

　　観測モデル

　 $p(x_n|z_n,C,\Sigma) = \mathcal{N}(Cz_n,\Sigma)$

先日記述した様にカルマン・ゲインを用いて解くと

　観測データ $x_n$ から観測前のデータ $z_n$ を得ることができます。　

mabonki0725.hatenablog.com

　次式がこの結論でした。

　　　 $p(z_n|x_n) = \mathcal{N}(\mu_n,V_n)$

　　 $\mu_n = A\mu_{n-1} + K_n(x_n - CA\mu_{n-1})$ 　

　　 $V_n = M = \left(I - K_nC \right) P_{n-1}$ 　

　　　但しカルマン・ゲインは

　　　　 $K_n = P_{n-1}C^T \left( CP_{n-1}C^T + \Sigma \right)^{-1}$

しかし解法式を見ると $A,\Gamma,C,\Sigma$ が所与として必要です。

　　下図は上式で $A,\Gamma,C,\Sigma$ を適当に設定しカルマン・フィルターで予測した時系列です。

　　推定された観測前のデータ $z_n$ で観測データの予測 $x_n,\dots,x_{n+t}$ をしているので予測精度が高いことが分ります。　　

　　　 f:id:mabonki0725:20170929231121p:plain

　この場合、対象時系列は１回前のトレンドを持つと考え、

　 ARモデルで $b_1 \sim b_4$ を計測し下式の様に変換行列 $A$ を設定しています。

　ノイズ項である $\Gamma$ と $\Sigma$ は適当に設定しました。　　

f:id:mabonki0725:20170929230347p:plain

この様な変換行列 $A$ をデータから推定できれば大変助かります。　

PRMLのカルマン・フィルターの学習ではこれら未決定項 $A \ C \ \Gamma \ \Sigma$ をデータから推定しています。

(1.1) 手法

PRMLではEMモデルでこの未決定項を推定しています。

系列データの確率は次式で与えられます。

　　　 $p(x_1,\dots,x_n,z_1,\dots,z_n) = p(z_1) \cdot \Pi_{k=2}^n p(z_k|z_{k-1}) \cdot \Pi_{k=1}^n p(x_k|z_k)$

　この対数を取ると

　　　 $\log(X,Z|\theta) = \log p(z_1|\mu_0,P_0) + \sum_{k=2}^n \log p(z_k|z_{k-1},A,\Gamma)$

$+ \sum_{k=1}^n \log p(x_k | z_k,C,\Sigma)$ 　 ①の式

　 1) Eステップでは

　　　 $Q(\theta,\theta^{old}) = \mathbb{E}_{z|old} \left(\log(X,Z|\theta) \right)$ ②の式

2)Mステップでは

　　 $A,\Gamma,C,\Sigma$ を $\theta$ として微分して最大化を行います。

　　ここでは最も重要な変換行列 $A$ を算出してみます。

　　 $A$ についての微分なので①の式で $A$ と $\Gamma$ 以外は定数となるので

　　期待値は

$Q(\theta,\theta^{old}) = -\frac{n}{2} - \mathbb{E}_{z|\theta^{old}} \left(\frac{1}{2} \sum _{k=1} ^ n (x_k - Az_k)^T \Gamma^{-1}(x_k - Az_k) \right) + const$ ③の式

　　これを微分して方程式を解くと

$\frac{\partial Q}{\partial A} = {\Gamma^{old}}^{-1} A \mathbb{E}(z_{k-1}z_{k-1}^T) +{\Gamma^{old}}^{-1} \mathbb{E}(z_k z_{k-1}^T)=0$

　　　 $A^{new} = \left( \sum_{k=1}^n x_n \mathbb{E}(z_k^T) \right) \cdot \left( \sum_{k=1}^n x_n \mathbb{E}(z_kz_k^T) \right)^{-1}$

$\Gamma^{new}$ も同様に微分して算出できます。

　　　　 $\Gamma^{new} = \frac{1}{n-1} \sum_{k=1}^n (\mathbb{E}(z_k z_k^T) - A^{new}\mathbb{E}(z_{k-1}z_k^T)$

$- \mathbb{E} (z_k z_{k-1}) {A^{new}}^T + A^{new}\mathbb{E}(z_{k-1}z_{k-1}^T) {A^{new}}^T )$

この結果をＥステップにいれて $A$ と $\Gamma$ が収束するまで繰返します。

2017-09-28

CNN最適化の制御式を生成するRNNの論文を読む

AI論文自然言語解析

ランニングできず　英語できず

(1) CNN最適化の制御式を生成するRNNの論文を読む

　「Neural Optimizer Search with Reinforcement Learning」

https://arxiv.org/abs/1709.07417

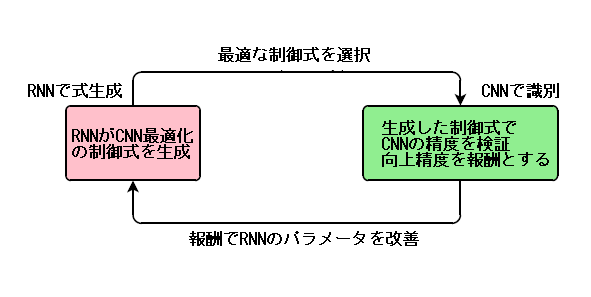
　CNNの最適化の制御式をRNNが強化学習で学習するモデルでかなり画期的なモデルです。

例えばCNNの最適化の仕様は次の様な重み調整の制御式で示す事ができます。

　　 $\Delta w = \hat{m} \ast (1+\epsilon) \ast sigmoid(10^{-4}w)$

$\Delta w = sign(m) \ast \sqrt{|g|}$

$\Delta w = sign(g) \ast sign(m) \ast \hat{m}$

$\Delta w = (1+sign(g) \ast sign(m)) * RMSProp$

ここで

$g$ は勾配 $\hat{m}$ は移動平均 $\epsilon$ はガウス

RNNが数式の構文を生成する性能に注目し、CNNが最適な精度を出せる様に制御式を強化学習するモデルとなります。

　　概念図は次となります。

f:id:mabonki0725:20170929000229p:plain

(1.1) 手法

　1) 制御式DSL(Domain Specific Language)の仕様

　深層学習の重み調整の制御式(DSL)は下記の単位 $\Delta w_i$ が繋がる形式で学習します。

　　 $\Delta w = \Delta w_1 \ast \Delta w_2 \ast \dots \Delta w_n$

$\Delta w_i = \lambda^i \ast b^i (u_1^i (op_1^i),u_2^i(op_2^i))$

ここで

　　　 $op_1 \ op_2$ はオペレータ

　　　 $u_1 \ u_2$ は関数(1引数)

　 $b$ はバイナリィ関数

　 $\lambda$ は学習率

　　制御式は図示すると次の様な構成となります

　　　　 f:id:mabonki0725:20170929122538p:plain

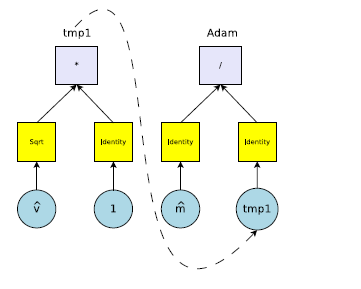
　以下に各種類の要素があります　　　

　　 f:id:mabonki0725:20170929122222p:plain

　 f:id:mabonki0725:20170929125027p:plain

　2) RNNの構成

　　制御式は5つの要素が１単位として連結した構成になります。

　　　 $\Delta w_i = \lambda^i \ast b^i (u_1^i (op_1^i),u_2^i(op_2^i))$

　 RNNでは上式は計算順序（逆ポーランド法)になっています。

f:id:mabonki0725:20170929123017p:plain

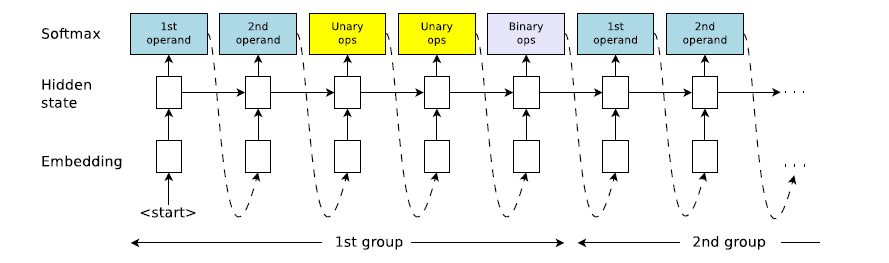
　3)強化学習によるRNNの学習

　　RNNの強化学習の記述は次式のみです。

　　 $J(\theta) = \mathbb{E}_{\Delta \sim p_\theta(\cdot)}\left( R(\Delta) \right)$

ここで

$J(\theta)$ は最大化する目的関数です

　　　 $R$ は制御式を投入した場合のCNN精度の改善幅を示しています

$\Delta \sim p_\theta(\cdot)$ は制御式の投入確率で $\theta$ でパラメータ化されています

　　但しこの強化学習は相当時間がかかるので様々な工夫をしています。

　　　・強化学習モデルはPPO(Proximal Policy Optimization)を採用

　　　・ＣＮＮは簡便な学習で済ます(2層、5回繰返)

　・組合わせの数は $10^6 \sim 10^{11}$ あるので無駄な組合わせを排除

　　それでも1日費やすとのことです。

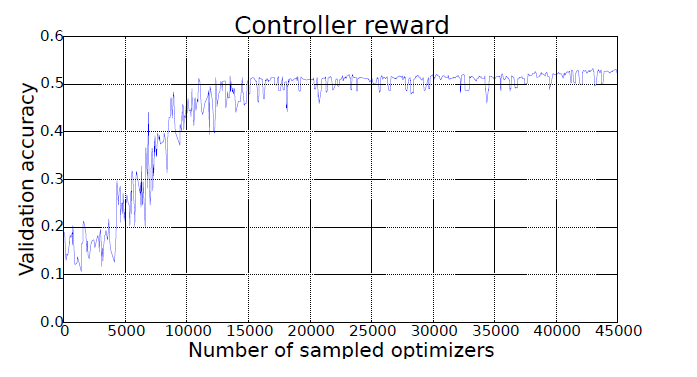
(1.2) 結果

　下図が強化学習を繰返しと簡便ＣＮＮによる精度の改善状態です。

　10000回で収束しています。データはCIFAR-10 CNN 　　　

f:id:mabonki0725:20170929124519p:plain

　　下表の様な重み調整の制御式と精度が達成されています。

　　識別モデルはwide-ResNet データはCIFAR-10

f:id:mabonki0725:20170929125847p:plain

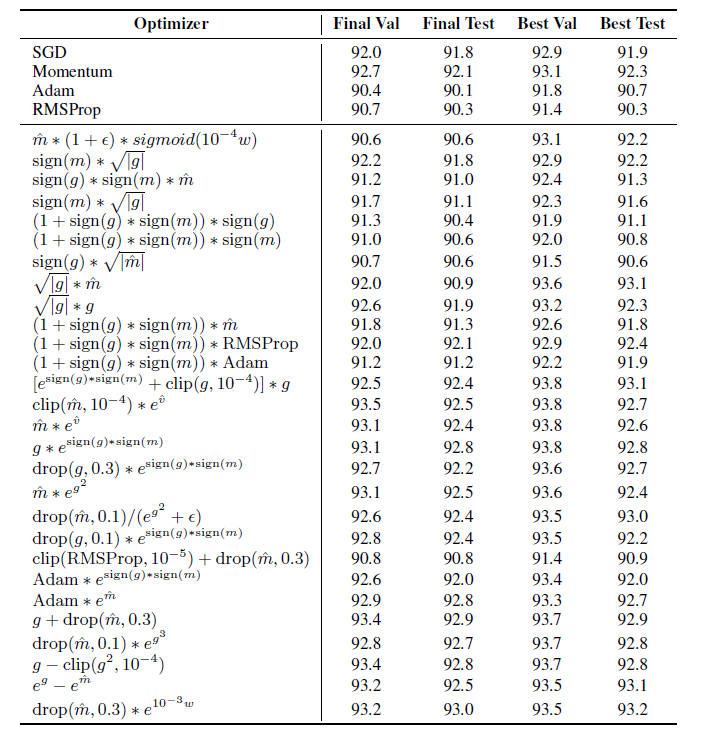
(1.3) 感想

　この論文では各制御式での重みの収束軌跡も添付しています。黒点が収束位置です。

　　　 f:id:mabonki0725:20170929131429p:plain

　素晴らしい成果と思います。この様な重み調整の制御式の試行が深層学習の解明に大きく寄与すると思えます。

2017-09-27

DeepMindの外部メモリーによる生成モデルの論文を読む

AI論文

ランニング30分英語できず

(1) DeepMindの外部メモリーによる生成モデルの論文を読む

「Variational Memory Addressing in Generative Models」https://arxiv.org/pdf/1709.07116.pdf

　この論文は深層学習の生成モデルVAEやGANで成果を出していることに対抗して、DeepMindが得意とする外部メモリを使ったより柔軟な生成モデルを提案したものです。

　 DeepMindはNTM(Neural Turing Machine)やDNC(Defferencial Neural Computer)で外部メモリーを組み込んだ推論を実現しており、この成果を生成モデルに応用しています。

　 VAEは生成データと実データの差をパラメータ化して深層学習で解消しますが、一方この論文の手法は外部メモリーに条件を設定し、この条件を満たすVAEを実現するものです。

　しかも下図(左)の様に生成データと実データの差を条件とすれば既存のVAEと同じ事が出来、大変柔軟性に富んだ手法となっています。

f:id:mabonki0725:20170927233809p:plain

(1.1) 手法

　VAEなので条件Ｍを満たす $x$ を生成する隠れ変数 $z$ を変分法で求めます。

　　 $p(x|M) = \sum_a p(a|M) \int p(z|m_a) p(x|z,m_a) dz$

　変分の下界は次式の右辺で、これが最大になる様に $z$ と $a$ を深層学習で訓練します。

　 $\log p(x|M) \ge \mathbb{E}_{a,z \sim q(\cdot |M,x)} \left( \log p(x,z,a | M) - \log q(a,z|M,x) \right)$

ここで

$a$ はMemory $M$ の番地

$a$ と $z$ は独立と見做せるので上式のサンプリング $\mathbb{E}_{a,z \sim q(\cdot |M,x)}$ の事後分布は次となります。

　　 $q(a,z|M,x) = q(a|M,x) \cdot q(z | m_a,x)$

　この論文は $q(a|M,x)$ と $q(z|m_a,x)$ の事後分布を各々解いています。

　1) $q(a|M,x)$ の事後分布

　　ここではNTMはDNCでの外部メモリーのキーの学習と同じ考え方を導入しています。

　　 $q(a|M,x) \propto \exp S_\phi^q(m_a,x)$

$S_\phi^q(m_a,x) = \frac{\lt e_a,e^q \gt}{{||e_a||}^2}$

ここで

　 $e_a = h_\phi(m_a)$ は外部メモリーの関数 $h_\phi$ による番地の隠れ変数

　 $e^q = h^q(x)$ は顕在データ $x$ の関数 $h^p$ による隠れ変数

即ち $x$ と $m_a$ の隠れ変数が近くなる様に関数 $h_\phi$ と $h^q$ を訓練した結果を

　　 $S_\phi^q$ として、これを事後分布 $q(a|M,x)$ としています。　

　2) $q(z|m_a,x)$ の事後分布

　　この事後分布は $m_a$ が離散なので簡単に計算できません。

　　そこでVIMCOというモデルで離散の事後分布を次式の変分で求めています。

　　 $\log(x) \ge \mathbb{E}_{a^{(k)} \sim q_\phi(a|x) \ z^{(k)} \sim q_\theta(z|m_a,x)} \left( \log \frac{1}{K} \sum_{k=1}^K \frac{p(x,m_a,z)}{q(a,z|x)} \right)$