2017-09-29

PRMLのカルマンフィルターの変換行列の学習を理解する

確率・統計

ランニングできず　英語できず

(1) PRMLのカルマンフィルターの変換行列の学習を理解する

　「PRML 13§ 13.3.2 Learing in LDS」

カルマンフィルターの状態方程式はシステムモデルと観測モデルに分離して表現されます。

f:id:mabonki0725:20170926203958p:plain

　システム・モデル

　　　　 $p(z_n|z_{n-1},A,\Gamma) = \mathcal{N}(A\mu_{n-1},P_{n-1})$

$p(z_{n-1}) = \mathcal{N}(\mu_{n-1},V_{n-1})$

但し $P_{n-1} =A V_{n-1}A^T + \Gamma$

　　観測モデル

　 $p(x_n|z_n,C,\Sigma) = \mathcal{N}(Cz_n,\Sigma)$

先日記述した様にカルマン・ゲインを用いて解くと

　観測データ $x_n$ から観測前のデータ $z_n$ を得ることができます。　

mabonki0725.hatenablog.com

　次式がこの結論でした。

　　　 $p(z_n|x_n) = \mathcal{N}(\mu_n,V_n)$

　　 $\mu_n = A\mu_{n-1} + K_n(x_n - CA\mu_{n-1})$ 　

　　 $V_n = M = \left(I - K_nC \right) P_{n-1}$ 　

　　　但しカルマン・ゲインは

　　　　 $K_n = P_{n-1}C^T \left( CP_{n-1}C^T + \Sigma \right)^{-1}$

しかし解法式を見ると $A,\Gamma,C,\Sigma$ が所与として必要です。

　　下図は上式で $A,\Gamma,C,\Sigma$ を適当に設定しカルマン・フィルターで予測した時系列です。

　　推定された観測前のデータ $z_n$ で観測データの予測 $x_n,\dots,x_{n+t}$ をしているので予測精度が高いことが分ります。　　

　　　 f:id:mabonki0725:20170929231121p:plain

　この場合、対象時系列は１回前のトレンドを持つと考え、

　 ARモデルで $b_1 \sim b_4$ を計測し下式の様に変換行列 $A$ を設定しています。

　ノイズ項である $\Gamma$ と $\Sigma$ は適当に設定しました。　　

f:id:mabonki0725:20170929230347p:plain

この様な変換行列 $A$ をデータから推定できれば大変助かります。　

PRMLのカルマン・フィルターの学習ではこれら未決定項 $A \ C \ \Gamma \ \Sigma$ をデータから推定しています。

(1.1) 手法

PRMLではEMモデルでこの未決定項を推定しています。

系列データの確率は次式で与えられます。

　　　 $p(x_1,\dots,x_n,z_1,\dots,z_n) = p(z_1) \cdot \Pi_{k=2}^n p(z_k|z_{k-1}) \cdot \Pi_{k=1}^n p(x_k|z_k)$

　この対数を取ると

　　　 $\log(X,Z|\theta) = \log p(z_1|\mu_0,P_0) + \sum_{k=2}^n \log p(z_k|z_{k-1},A,\Gamma)$

$+ \sum_{k=1}^n \log p(x_k | z_k,C,\Sigma)$ 　 ①の式

　 1) Eステップでは

　　　 $Q(\theta,\theta^{old}) = \mathbb{E}_{z|old} \left(\log(X,Z|\theta) \right)$ ②の式

2)Mステップでは

　　 $A,\Gamma,C,\Sigma$ を $\theta$ として微分して最大化を行います。

　　ここでは最も重要な変換行列 $A$ を算出してみます。

　　 $A$ についての微分なので①の式で $A$ と $\Gamma$ 以外は定数となるので

　　期待値は

$Q(\theta,\theta^{old}) = -\frac{n}{2} - \mathbb{E}_{z|\theta^{old}} \left(\frac{1}{2} \sum _{k=1} ^ n (x_k - Az_k)^T \Gamma^{-1}(x_k - Az_k) \right) + const$ ③の式

　　これを微分して方程式を解くと

$\frac{\partial Q}{\partial A} = {\Gamma^{old}}^{-1} A \mathbb{E}(z_{k-1}z_{k-1}^T) +{\Gamma^{old}}^{-1} \mathbb{E}(z_k z_{k-1}^T)=0$

　　　 $A^{new} = \left( \sum_{k=1}^n x_n \mathbb{E}(z_k^T) \right) \cdot \left( \sum_{k=1}^n x_n \mathbb{E}(z_kz_k^T) \right)^{-1}$

$\Gamma^{new}$ も同様に微分して算出できます。

　　　　 $\Gamma^{new} = \frac{1}{n-1} \sum_{k=1}^n (\mathbb{E}(z_k z_k^T) - A^{new}\mathbb{E}(z_{k-1}z_k^T)$

$- \mathbb{E} (z_k z_{k-1}) {A^{new}}^T + A^{new}\mathbb{E}(z_{k-1}z_{k-1}^T) {A^{new}}^T )$

この結果をＥステップにいれて $A$ と $\Gamma$ が収束するまで繰返します。

2017-09-28

CNN最適化の制御式を生成するRNNの論文を読む

AI論文自然言語解析

ランニングできず　英語できず

(1) CNN最適化の制御式を生成するRNNの論文を読む

　「Neural Optimizer Search with Reinforcement Learning」

https://arxiv.org/abs/1709.07417

　CNNの最適化の制御式をRNNが強化学習で学習するモデルでかなり画期的なモデルです。

例えばCNNの最適化の仕様は次の様な重み調整の制御式で示す事ができます。

　　 $\Delta w = \hat{m} \ast (1+\epsilon) \ast sigmoid(10^{-4}w)$

$\Delta w = sign(m) \ast \sqrt{|g|}$

$\Delta w = sign(g) \ast sign(m) \ast \hat{m}$

$\Delta w = (1+sign(g) \ast sign(m)) * RMSProp$

ここで

$g$ は勾配 $\hat{m}$ は移動平均 $\epsilon$ はガウス

RNNが数式の構文を生成する性能に注目し、CNNが最適な精度を出せる様に制御式を強化学習するモデルとなります。

　　概念図は次となります。

f:id:mabonki0725:20170929000229p:plain

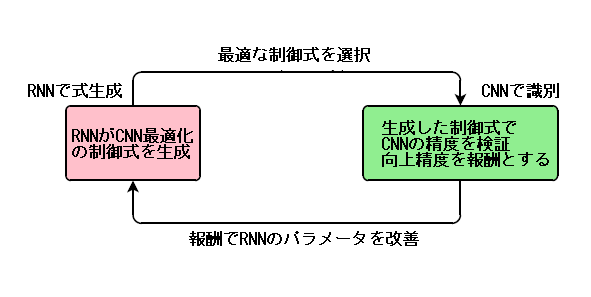
(1.1) 手法

　1) 制御式DSL(Domain Specific Language)の仕様

　深層学習の重み調整の制御式(DSL)は下記の単位 $\Delta w_i$ が繋がる形式で学習します。

　　 $\Delta w = \Delta w_1 \ast \Delta w_2 \ast \dots \Delta w_n$

$\Delta w_i = \lambda^i \ast b^i (u_1^i (op_1^i),u_2^i(op_2^i))$

ここで

　　　 $op_1 \ op_2$ はオペレータ

　　　 $u_1 \ u_2$ は関数(1引数)

　 $b$ はバイナリィ関数

　 $\lambda$ は学習率

　　制御式は図示すると次の様な構成となります

　　　　 f:id:mabonki0725:20170929122538p:plain

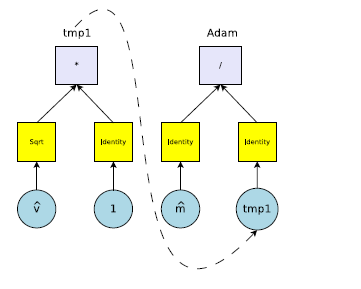
　以下に各種類の要素があります　　　

　　 f:id:mabonki0725:20170929122222p:plain

　 f:id:mabonki0725:20170929125027p:plain

　2) RNNの構成

　　制御式は5つの要素が１単位として連結した構成になります。

　　　 $\Delta w_i = \lambda^i \ast b^i (u_1^i (op_1^i),u_2^i(op_2^i))$

　 RNNでは上式は計算順序（逆ポーランド法)になっています。

f:id:mabonki0725:20170929123017p:plain

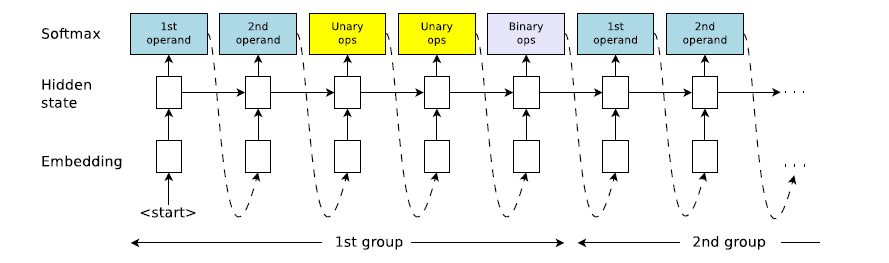
　3)強化学習によるRNNの学習

　　RNNの強化学習の記述は次式のみです。

　　 $J(\theta) = \mathbb{E}_{\Delta \sim p_\theta(\cdot)}\left( R(\Delta) \right)$

ここで

$J(\theta)$ は最大化する目的関数です

　　　 $R$ は制御式を投入した場合のCNN精度の改善幅を示しています

$\Delta \sim p_\theta(\cdot)$ は制御式の投入確率で $\theta$ でパラメータ化されています

　　但しこの強化学習は相当時間がかかるので様々な工夫をしています。

　　　・強化学習モデルはPPO(Proximal Policy Optimization)を採用

　　　・ＣＮＮは簡便な学習で済ます(2層、5回繰返)

　・組合わせの数は $10^6 \sim 10^{11}$ あるので無駄な組合わせを排除

　　それでも1日費やすとのことです。

(1.2) 結果

　下図が強化学習を繰返しと簡便ＣＮＮによる精度の改善状態です。

　10000回で収束しています。データはCIFAR-10 CNN 　　　

f:id:mabonki0725:20170929124519p:plain

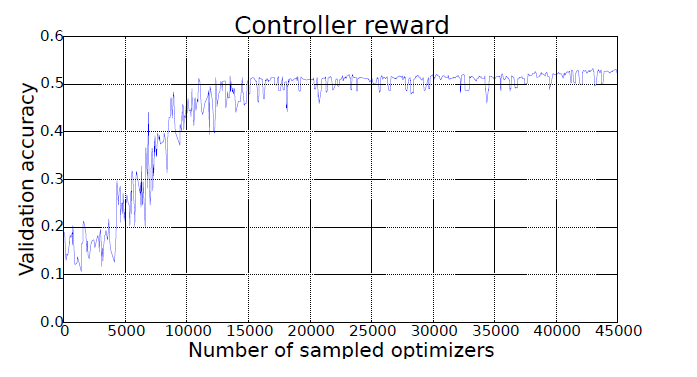
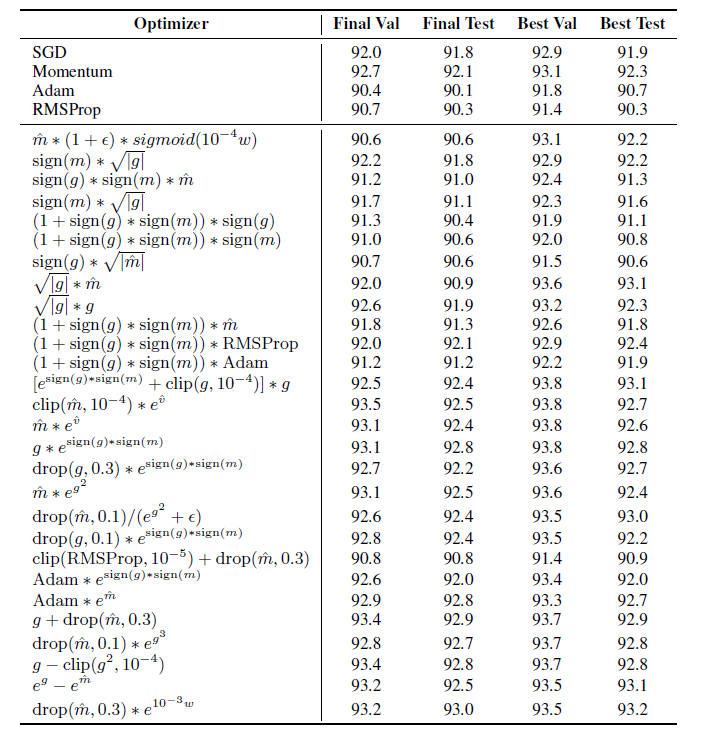
　　下表の様な重み調整の制御式と精度が達成されています。

　　識別モデルはwide-ResNet データはCIFAR-10

f:id:mabonki0725:20170929125847p:plain

(1.3) 感想

　この論文では各制御式での重みの収束軌跡も添付しています。黒点が収束位置です。

　　　 f:id:mabonki0725:20170929131429p:plain

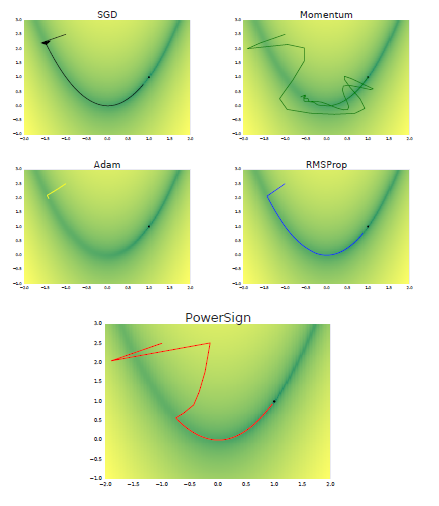
　素晴らしい成果と思います。この様な重み調整の制御式の試行が深層学習の解明に大きく寄与すると思えます。

2017-09-27

DeepMindの外部メモリーによる生成モデルの論文を読む

AI論文

ランニング30分英語できず

(1) DeepMindの外部メモリーによる生成モデルの論文を読む

「Variational Memory Addressing in Generative Models」https://arxiv.org/pdf/1709.07116.pdf

　この論文は深層学習の生成モデルVAEやGANで成果を出していることに対抗して、DeepMindが得意とする外部メモリを使ったより柔軟な生成モデルを提案したものです。

　 DeepMindはNTM(Neural Turing Machine)やDNC(Defferencial Neural Computer)で外部メモリーを組み込んだ推論を実現しており、この成果を生成モデルに応用しています。

　 VAEは生成データと実データの差をパラメータ化して深層学習で解消しますが、一方この論文の手法は外部メモリーに条件を設定し、この条件を満たすVAEを実現するものです。

　しかも下図(左)の様に生成データと実データの差を条件とすれば既存のVAEと同じ事が出来、大変柔軟性に富んだ手法となっています。

f:id:mabonki0725:20170927233809p:plain

(1.1) 手法

　VAEなので条件Ｍを満たす $x$ を生成する隠れ変数 $z$ を変分法で求めます。

　　 $p(x|M) = \sum_a p(a|M) \int p(z|m_a) p(x|z,m_a) dz$

　変分の下界は次式の右辺で、これが最大になる様に $z$ と $a$ を深層学習で訓練します。

　 $\log p(x|M) \ge \mathbb{E}_{a,z \sim q(\cdot |M,x)} \left( \log p(x,z,a | M) - \log q(a,z|M,x) \right)$

ここで

$a$ はMemory $M$ の番地

$a$ と $z$ は独立と見做せるので上式のサンプリング $\mathbb{E}_{a,z \sim q(\cdot |M,x)}$ の事後分布は次となります。

　　 $q(a,z|M,x) = q(a|M,x) \cdot q(z | m_a,x)$

　この論文は $q(a|M,x)$ と $q(z|m_a,x)$ の事後分布を各々解いています。

　1) $q(a|M,x)$ の事後分布

　　ここではNTMはDNCでの外部メモリーのキーの学習と同じ考え方を導入しています。

　　 $q(a|M,x) \propto \exp S_\phi^q(m_a,x)$

$S_\phi^q(m_a,x) = \frac{\lt e_a,e^q \gt}{{||e_a||}^2}$

ここで

　 $e_a = h_\phi(m_a)$ は外部メモリーの関数 $h_\phi$ による番地の隠れ変数

　 $e^q = h^q(x)$ は顕在データ $x$ の関数 $h^p$ による隠れ変数

即ち $x$ と $m_a$ の隠れ変数が近くなる様に関数 $h_\phi$ と $h^q$ を訓練した結果を

　　 $S_\phi^q$ として、これを事後分布 $q(a|M,x)$ としています。　

　2) $q(z|m_a,x)$ の事後分布

　　この事後分布は $m_a$ が離散なので簡単に計算できません。

　　そこでVIMCOというモデルで離散の事後分布を次式の変分で求めています。

　　 $\log(x) \ge \mathbb{E}_{a^{(k)} \sim q_\phi(a|x) \ z^{(k)} \sim q_\theta(z|m_a,x)} \left( \log \frac{1}{K} \sum_{k=1}^K \frac{p(x,m_a,z)}{q(a,z|x)} \right)$

　　　ここで $k$ は離散のインデックスです

　　右辺を各々 $\theta$ と $\phi$ を微分して下界を最大化しています。

この辺までの記述になるとかなり式の展開が曖昧になっています。

(1.2) 結果

　下図は学習された番地毎のメモリーの状態 $m_a$ が示してあり、正解の図 $x$ と推定された番地 $p(a|x)$ の画像が近いことが分ります。

f:id:mabonki0725:20170928085531p:plain

2017-09-26

PRMLのカルマン・フィルターの理論を理解する

確率・統計

ランニングできず　英語できず

(1) PRMLのカルマン・フィルターの理論を理解する

「PRML §13.3 Linear Dynamic System」

　Openposeの多関節の動画は多次元の時系列のため、多次元時系列が解析できる次の開発済みのモデルで性能比較を行うことにしました。

　　・隠れマルコフ

　　・カルマンフィルター

　　・LSTM

　　・SCW(Soft Confidense Weight)

f:id:mabonki0725:20170926195839p:plain

　ここで既存のカルマン・フィルターを古い有本先生のモデルからPRMLのLDSモデルに変更することにしました。ここでPRMLの記述に従ってカルマン・ゲインを使った導出まで行います。

　PRMLの最も重大な公式は次の正規分布の周辺分布と事後分布であることはPRMLで随所に参照される公式なので明らかです。

　　　 $p(x)=\mathcal{N}(x|\mu,\Lambda^{-1})$ 事前分布(2.113)

　　　 $p(y|x) = \mathcal{N}(y | Ax + b,L^{-1})$ 　尤度分布(2.114)

　　 $\Downarrow$

　　　 $p(y) = \int p(y|x) p(x) dx = \mathcal{N}(y |A\mu + b, L^{-1} + A \Lambda^{-1}A^T)$ 周辺分布(2.115)

　　 $p(x|y) = \mathcal{N}(x | \Sigma (A^TL(y-b)+\Lambda\mu),\Sigma)$ 事後分布(2.116)

　　但し $\Sigma=(A + A^TLA)^{-1}$

ここで各変数の変遷過程は下図となります。

　カルマン・フィルターは観測データ $x_n$ から観測前のデータ $z_n$ を求めるベイズモデルであることが分ります。

f:id:mabonki0725:20170926203958p:plain

　　 $p(z_n) = \mathcal{N}(z_n|\mu_n,V_n)$

$p(x) = \int p(x_n | z_n) \left(\int p(z_n|z_{n-1}) p(z_{n-1})dz_{n-1} \right) dz_n$

ここで

　　　 $p(x_n|z_n)$ は観測器による変換

$p(z_n|z_{n-1})$ は変換器による変遷

これを正規分布に置き換えると

　　 $p(x_n|z_n) = \mathcal{N}(x_n|Cz_n,\Sigma) \cdot \int \mathcal{N}(z_n | Az_{n-1},\Gamma) \mathcal{N}(z_{n-1}|\mu_{n-1},V_{n-1}) dz_{n-1}$

ここで右辺の積分式に(2.115)の周辺分布の公式を使うと

　 $\int \mathcal{N}(z_n | Az_{n-1},\Gamma) \mathcal{N}(z_{n-1}|\mu_{n-1},V_{n-1}) dz_{n-1} = \mathcal{N}(z_n | A\mu_{n-1},P_{n-1})$ 　Ａ式

但し $P_{n-1} = AV_{n-1}A^T + \Gamma$

これより観測データ $x_n$ から実態データ $z_n$ を事後分布の公式で計算します。

$p(z_n) = \mathcal{N}(z_n | A\mu_{n-1},P_{n-1})$ 事前分布Ａ式より

　　 $p(x_n|z_n) = \mathcal{N}(x_n|Cz_n,\Sigma)$ 　　尤度分布

　上式に(2.117)の事後分布の公式を使うと

$p(z_n|x_n) = \mathcal{N}(x_n|M(C^T\Sigma^{-1}x_n + P_{n-1}^{-1}A\mu_{n-1}),M)$ 　①式

但し $M=(P_{n-1} + C^T\Sigma C)^{-1}$ 　②式

ここでPRMLの巻末にある重要な逆行列式の公式(C.7)を使います

　 $\left( A+BD^{-1}C\right)^{-1} = A^{-1} - A ^{-1}B(D+CA^{-1}B)^{-1}CA^{-1}$ (C.7)

$M=(P_{n-1} + C^T\Sigma C)^{-1} = P_{n-1} - P_{n-1} C^T \left(\Sigma + CP_{n-1}C^T \right)^{-1}CP_{n-1}$

ところでMは次のカルマンゲイン $K_n$ を使うと③式の様になります。

　　　 $K_n = P_{n-1}C^T \left( CP_{n-1}C^T + \Sigma \right)^{-1}$

$M = P_{n-1} - P_{n-1} C^T \left(\Sigma + CP_{n-1}C^T \right)^{-1}CP_{n-1}$

$M=\left(I - P_{n-1}C^T(\Sigma + CP_{n-1}C^T )^{-1}C \right) P_{n-1}$

$M= \left(I - K_nC \right) P_{n-1}$ ③式

　また②式より　　

　　 $MC^T\Sigma^{-1} = (P_{n-1} + C^T\Sigma C)^{-1} \cdot C^T \Sigma^{-1}$

$MC^T\Sigma^{-1} = P_{n-1}C^T(CP_{n-1}C^T + \Sigma)^{-1} = K_n$ 　④式

また事後分布①式の平均は③式と④式を入れると

$M(C^T\Sigma^{-1}x_n + P_{n-1}^{-1}A\mu_{n-1})=MC^T\Sigma^{-1}x_n + (I-K_nC)A\mu_{n-1}$

$= K_nx_n + A\mu_{n-1} - K_nCA\mu_{n-1}$

$= A\mu_{n-1} + K_n(x_n - CA\mu_{n-1})$ ⑤式

最終的に観測値 $x_n$ とカルマン・ゲイン $K_n$ を使って実態 $z_n$ はの平均 $\mu_n$ と分散 $V_n$ は次式で求められた。

$p(z_n|x_n) = \mathcal{N}(\mu_n,V_n)$

　 $\mu_n = A\mu_{n-1} + K_n(x_n - CA\mu_{n-1})$ 　⑤式より

　 $V_n = M = \left(I - K_nC \right) P_{n-1}$ 　③式より

2017-09-25

深層生成による暗黒物質探査の論文を読む

AI論文画像認識

テニス２時間　英語できず

(1)深層生成による暗黒物質探査の論文を読む

　「Enabling Dark Energy Science of with Deep Generative Models of Galaxy Images」

https://arxiv.org/abs/1609.05796

　宇宙の80％を占めると云われている暗黒物質は宇宙膨張の謎を解く鍵とされていますが、観測が難しいので実態が不明なままです。この実態は下図の黒い部分の様に銀河の光を通して間接的に観測します。具体的には重力レンズという理論で銀河の光の歪みを観測して暗黒物質の規模を推定しています。しかし銀河の光の歪みを計測することも難しいので、VAEやGANを使って銀河の画像を補正しようとする論文です。

f:id:mabonki0725:20170925204115p:plain

(1.1) 手法

　ここでは条件付VAEと条件付GANの２種類で銀河の画像を生成しています。

　　条件付VAEは良く似ていますが半教師学習のSemi-VAEではありません。

　　　画像に一部のみラベルが付いている場合がSemi-VAEです。

　データとしては8500個の銀河の画像(64×64) $x$ と条件ベクトル $y$ をもつCOSMOSデータで訓練します。

条件ベクトル $y$ は３の特徴量（銀河のサイズ、明るさ、宇宙距離）のみです

1) C-VAE(conditional VAE)

VAEなので隠れ変数 $z$ を仮定します。 $z$ は具体的には多変量の平均と分散を表します。

VAEはデータ $\mathcal{D}=(\hat{x}^1,\hat{y}^1),\dots,(\hat{x}^N,\hat{y}^N)$ から次の生成モデルの隠れ変数 $z$ 及びパラメータ $\theta_1 \ \theta_2$ を求めることになります。

　 $p_\theta(x,z | y) = p_{\theta_1}(x | z,y) p_{\theta_2}(z | y)$

隠れ変数 $z$ を媒介とする変分の教科書は以下なので

　 $\log p(x) = \int q(z) \log \frac{p(x,z)}{q(z)} dz - \int q(z) \log \frac{p(z|x)}{q(z)} dz$

$\log p(x) \ge \mathbb{E}_{z \sim q(z)} ( \log p(x | z)) - \mathbb{D}_{KL}(p(z|x) || q(z))$

　　ここで

　　　 $\int q(z) \log \frac{p(x,z)}{q(z)} dz \ge \int q(z) \log \frac{p(x,z)}{p(z)} dz = \mathbb{E}_{z \sim q(z)} ( \log p(x | z))$

を使った

隠れ変数 $z$ を使った $p_\theta(\hat{x}|\hat{y})$ の対数尤度の変分は次式で定義できます。

　　 $\log p_\theta(\hat{x} | \hat{y}) \ge -\mathbb{D}_{KL} \left(q_\phi(z | \hat{x},\hat{y}) || p_{\theta_1}(z | \hat{y}) \right) + \mathbb{E}_{z \sim q_\phi} \left( \log p_{\theta_2}(\hat{x} | z,\hat{y}) \right)$

　 VAEの損失関数 $\mathcal{L}$ が最小となる隠れ変数 $z$ 及びパラメータ $\phi \ \theta_1 \ \theta_2$ を深層学習で算出します

　 $\mathcal{L}(\phi,\theta_1,\theta_2,\hat{x},\hat{y}) = \mathbb{D}_{KL} \left(q_\phi(z | \hat{x},\hat{y}) || p_{\theta_1}(z | \hat{y}) \right) - \mathbb{E}_{z \sim q_\phi} \left( \log p_{\theta_2}(\hat{x} | z,\hat{y}) \right)$

2) C-GAN(conditnal GAN)

条件付敵対的生成モデルGANでは次式で定式化できます。

　 $min_w max_\psi \mathbb{E}_{\hat{x},\hat{y} \in \mathcal{D}} \left( \log(D_\psi(\hat{x},\hat{y}) + \log(1 - D_\psi(G_w(z,\hat{y}),\hat{y})) \right)$

ここで

このGANは隠れ変数 $z$ の介在で解けないので $z \sim \mathcal{U}(0,1)$ で一様乱数としています

　 $G_w(z,\hat{y})$ は生成器 C-VAEの $p_{\theta_2}(x | z,y)$ を使います

$D_\psi(\hat{x},\hat{y})$ は一般の識別器

(1.2) 結果

　　COSMOSデータ（特徴量３個）についてRealが銀河の実写で C-VAEとC-GANが生成結果です。

　　生成結果は何れもノイズが除去されています。

f:id:mabonki0725:20170925214726p:plain

　　GALAXY-ZOOデータでGANで生成した結果です。但しこのデータの特徴量 $y$ は37個のベクトルですので、精緻画像が得られています。

f:id:mabonki0725:20170925215532p:plain

2017-09-24

深層強化学習によるChatbotモデルの論文を読む

AI論文自然言語解析

ランニング30分　英語：movie 2012

(1) 深層強化学習によるChatbotモデルの論文を読む

　「A Deep Reinforcement Learning Chatbot」https://arxiv.org/abs/1709.02349

　この論文はアマゾンの2017年の人工知能モデル競技会で開発された応答会話モデルMILABOTの詳細な報告です。

　このモデルはありとあらゆる自然言語モデルと自然言語特徴量の寄せ集めで百科事典的なモデルとなっています。

　概要としては以下となります。　

　　・アマゾンが提供する「Amazon Mechanical Turk」で人間による20万件の会話格付を教師データとして利用　Amazon Mechanical Turk – クラウドソーシング用のマーケットプレイス | AWS

　　・既存の22の会話モデルで応答の候補を生成します。

　　　この22の会話モデルには、次の様々なモデルが組込んであります

　　　　用途別(映画/検索）

　　　　手法別（テンプレート法/LSTM/機械学習）

　　　また主要なモデルにはアルゴリズムとモデルインストールサイトが添付されています

　　・応答候補の中で最適な応答が無ければ、強化学習で最優良な応答を選択して返します

　　・候補応答毎について格付予測を深層学習モデルで行っています

　　　深層学習は自然言語の特徴を1458と14万件の格付の教師データで学習しています。　

　　　1458の特徴量の仕様が記述されています　　

f:id:mabonki0725:20170926052518p:plain

　　・会話は互いの応答で成立するので、最終会話までの評価をする必要があります。

　　　予測格付を報酬として深層強化学習で最終会話までの累計報酬の価値関数を計算して、

　　　累計報酬の最大価値をもつ応答候補が選択されます

　　　深層強化学習は自然言語の特徴量23個と累計報酬とで価値関数を解いています

　　　　 $\hat{\phi} = argmax_\phi \sum_d \sum_t \left( Q_\phi (h_t^d,a_t^d) - R^d \right)^2$

ここで　

$\phi$ は深層強化学習のパラメータ

　　　 $d$ は会話(dialog)

$R$ は会話の予想格付

$h_t^d \ a_t^d$ は会話暦と選択した応答

$Q_\phi = \phi_0 + \phi_1 \cdot feature_1 + \dots + \phi_{23} \cdot feature_{23}$

　概念図としては以下となります。　　

f:id:mabonki0725:20170925051653p:plain

2017-09-23

プレイヤーと環境とが敵対的に学習する論文を読む

AI論文ロボテックス

ランニングできず　英語できず

(1) プレイヤーと環境とが敵対的に学習する論文を読む

　「Learning to Design Games: Strategic Environments　in Reinforcement Learning」

https://arxiv.org/abs/1707.01310v2

　この論文は強化学習でプレイヤーと活動する環境とが敵対的に競争し合ってプレイヤーの能力を高めるものです。

この論文のコンセプトとして下図を示しています。

f:id:mabonki0725:20170923191740p:plain

　一般道の自動運転では様々な連続的に生起する事象を回避する必要があり、その模擬は大変難しいことが知られています。この論文は運転者とその走行環境を互いに複雑にして運転能力を高める方法を開くものと考えられます。

　この論文では下図の様にプレイヤーと迷路を敵対的に進化させて同時に学習をすることができています。

f:id:mabonki0725:20170923182455p:plain

(1.1) 手法

　強化学習のBellman方程式に敵対的学習を達成するminmaxが定式化されています。

　 $(\theta^*,\phi) = argmin_\theta \ max_\phi \mathbb{E}\left( G|\pi_\phi,M_\theta= \lt S,A,P_\theta,R,\gamma \gt \right)$

ここで

　　 $\theta$ は遷移確率 $P$ のパラメータで報酬を最小化します

$\phi$ はプレイヤーの方策 $/pi$ パラメータで報酬を最大化します

$G$ は累計報酬

$S \ A \ R \ \gamma$ は状態、行動(前後左右移動)、報酬、割引率です

　　 $P_\theta$ は遷移確率

$\pi_\phi$ は方策

　 $\theta$ と $\phi$ は微分して計算して最大傾斜となる値に修正します。

$\theta_{i+1} = \theta_i + \eta \cdot \nabla \theta \cdot \mathbb{E}$

$\phi_{i+1} = \phi_i + \eta \cdot \nabla \phi \cdot \mathbb{E}$

但し、 $\phi$ は上式で求めてますが、迷路を複雑にする $\theta$ は報酬 $G$ を最小にする2重の期待値を取る式となっていて相当困難な式が展開されています。結局擬似プログラムをAppendixに添付しています。

$\theta \sim p(\mu_w)$

　　 $w^* = argmin_w \mathbb{E}_{\theta \sim \mu_w} \left ( \mathbb{E} (G|\pi_{\phi^*}; M_\theta^A = \lt S^A,A^A,P_\theta^A,R^A,\gamma^A \gt )\right)$

(1.2) 結果

　複数のモデルについてプレイヤーと迷路を同時に高度化しています。

　ここで

　　Roundは計算の繰返回数　Returnは迷路での折返し回数です。

　　OPTはプレイヤーが学習しないモデル

　　DFSは判断木を生成して深さ優先で最適判断するモデル

　　RHSは判断木を生成して右方向優先で最適判断するモデル

　　DQNはDeep Q-learningです

　この結果ではDQNのプレイヤーが最適な学習をするので早期に複雑な迷路を生成しています。

f:id:mabonki0725:20170923185215p:plain