砂のトラックを走行する実自動車での強化学習の論文を読む

下図の様な砂のトラックを走行する自動運転ではアクセルやハンドルの伝達誤差また砂利面との滑りや摩擦があり、予想し得ない事象が頻発すると想定する必要がある。下記の論文は実際の自動車での強化学習をMPPI(Model Predictiv Path Integral)と云う手法で実験した論文を読んでみる。

https://www.cc.gatech.edu/~bboots3/files/InformationTheoreticMPC.pdf

f:id:mabonki0725:20190125190450p:plain

DQNやActor-Criticの様なModel-freeモデルでは、環境から持続的な特徴量の変化を抽出して最大報酬を得る様に行動決定のパラメータを調整するが、様々な原因で変異や誤差がある環境では学習に相当時間(2,3日)かかる事が報告されている。一方で実際の課題に沿ったモデル化から最適化を図るModel-Baseモデルは学習効果が著しいとされる[1]。

(1) モデル

　この論文は対象を限定せず制御誤差があり罰則(コスト)が設定されている動作物体の最適操作について汎用的に記述しているが、具体的にトラックを周回する自動運転での説明とする。

　動力エンジンの機構や地面との摩擦等により操作が自動車の制御機能に伝達するには誤差があるとして、その誤差を多変量正規分布とする。コストはゴール前の離脱やトラック(走行路)を逸脱すると与えられるとする。この論文では、この様な条件でコストを最小化する経路上の操作量 $u$ を求める。

(1-1) 状態遷移モデルの定義　

状態 $x$ の遷移過程は次の関数とし、具体的には観測された状態 $x$ と操作 $u$ の記録により全結合のニューロで学習する。

　 $x_{t+1} = F(x_t,v_t)$ 　 $s.t$ $v_t = \mathcal{N}(u_t,\Sigma)$ (1)

ここで

　　　 $x_t$ は時刻 $t$ での状態

　　　 $u_t$ は運転操作の量（アクセル、ブレーキ、ハンドル回転量)

$v_t$ は実際に自動車に伝わる制御分布。平均は $u_t$ で分散を $\Sigma$ とする正規分布　

　　　 $F$ は状態遷移関数で全結合のニューロで学習される。

(1-2) 操作と制御の分布およびコスト関数の定義

　以下ではコスト関数の自由エネルギーの最小化を考え、経路上の時刻 $t$ での操作量 $u_t$ を次の(8)式から(26)式で求める。

　ここで制御の経路 $V={v_0,\dots,v_T}$ を使って以下の定義をする。

　　・制御の分布

　　　 $p(V) = \pi_{t=0}^{T-1} Z^{-1} \exp(-\frac{1}{2} v_t^T \Sigma^{-1} v_t)$ (2)

・運転誤差の分布

　　　 $q(V) = \pi_{t=0}^{T-1} Z^{-1} \exp(-\frac{1}{2} (v_t-u_t)^T \Sigma^{-1} (v_t-u_t))$ 　 (3)

・コスト関数

　　　 $S(V) = C(x_1,\dots,x_T) = \phi(x_T) + \sum_{t=1}^{T-1}q(x_t)$ (6)

　　ここで $\phi$ はゴールに失敗のコストで $q(x_t)$ は状態 $x_t$ でのコスト

(1-3)コスト関数の自由エネルギーの導入

ここで制御の分布 $p(V)$ について期待値を取ったコスト関数の自由エネルギーを定義して、この最小化によりコストが最小になる操作 $u$ を推定する。この手法については文献[2]が詳しい。

　　　 $\mathcal{F}(V) = -\lambda \log ( \mathbb{E_p} [\exp (-\frac{1}{\lambda} S(V) ) ] )$ (8)

　上式の自由エネルギーを運転誤差の分布 $q(V)$ についての期待値に変換する。

　　 $\mathcal{F}(V) = -\lambda \log ( \mathbb{E_q} [\frac{p(V)}{q(V)} \exp (-\frac{1}{\lambda} S(V) )])$ 　 (9)

ここで $\mathbb{E_p}[f(x)] = \int p(v) f(x) dv = \int q(v) f(x) \frac{p(v)}{q(v)} d v =\mathbb{E_q}[\frac{p(V)}{q(V)} f(x)]$ を使った。

　(9)式はJensenの不等式を使うと $log$ が期待値の中に入り次式になる

　 $\mathcal{F}(V) \ge -\lambda ( \mathbb{E_q} [\log \frac{p(V)}{q(V)} \exp (-\frac{1}{\lambda} S(V) )])$ 　 (10)

　式(10)で操作誤差分布が次の時、両辺とも定数になり不等式が一致するので自由エネルギーが最小になる。

　 $q^*(V) = \frac{1}{\eta} \exp(\frac{1}{\lambda} S(V)) p(V)$ (14)

　　　ここで $\eta$ は分配関数で $q^*(V)$ を確率０～１にしている。　　

上式を(9)と(10)式に投入するとJensenの不等式が一致することが分る。

　　　 $\mathcal{F}(V) = -\lambda \log (\mathbb{E_q} [ \eta ]) = -\lambda \log \eta$

　 $-\lambda ( \mathbb{E_q} [\log \frac{p(V)}{q(V)} \exp (-\frac{1}{\lambda} S(V) )] = -\lambda ( \mathbb{E_q} [ \log \eta] = -\lambda \log \eta$

　そこで全経路について(14)式にできるだけ一致する操作 $u$ を $\mathbb{D}_{KL}$ で求める。

　　　 $u^* = min_{u} \mathbb{D}_{KL} (q^*(V) || q(V))$

　経路 $V$ の集合 $\tau$ では $\mathbb{D}_{KL}$ の定義より次の様になる。

　　　 $\int_\tau q^*(V) \log (\frac{q^*(V)}{q(V)}) dV$

$=\int_\tau q^*(V) \log (\frac{q^*(V) p(V)} {p(V) q(V)}) dV$

$=\int_\tau q^*(V) \log (\frac{q^*(V)}{p(V)}) - q^*(V) \log (\frac{q(V)}{p(V)}) dV$

　上式の第一項で $q^*(V)$ は(14)式、 $p(V)$ は(2)式より操作 $u$ と無関係なので

　上式の第二項を最大化すれば最適な $u$ が求まる。

　　　 $u^* = max_u \int_\tau q^*(V) \log (\frac{q(V)*}{p(V)}) dV$ (16)

(16)式の中の $\frac{q(V)*}{p(V)}$ は定義(2)と(3)式より以下となる。

　　　 $\frac{q(V)}{p(V)}=\exp (\sum_{t=0}^{T-1} - \frac{1}{2} u_t^T \Sigma^{-1}u_t + u_t^T \Sigma^{-1}v_t )$ 　　(17)

(16)式は以下に変形できる。

　　　 $\int_\tau q^*(V) [\exp(\sum_{t=0}^{T-1} - \frac{1}{2} u_t^T \Sigma^{-1}u_t + u_t^T \Sigma^{-1}v_t) ] dV$ 　　(18)

(18)式を $\mathcal{G}(u)$ と置き $u$ について微分すると

　　　 $\mathcal{G}(u) = \sum_{t=0}^{T-1} ( \frac{1}{2} u_t^T \Sigma^{-1} u_t + u_t^T\int_\tau q^*(V) v_t dV)$ (19)

$\frac{d \mathcal{G}(u)}{d u} = -\Sigma^{-1}u_t + \int_\tau \Sigma^{-1} q*(V) v_t dV$

　上式を０とすると操作 $u$ の最適下は以下となる

　　　 $u^*_t = \int_\tau q^*(V) v_t dV$ 　　　(20)

(1-4) 実装のためのImportanceサンプリング手法の導入

　ここからは(20)式を実用的に使うため次式に変形してImportanceサンプリング $w(V)$ 導入する。

　　　 $u^*_t = \int_\tau q(V) \frac{q^*(V)}{p(V)} \frac{p(V)}{q(V)} v_t dV$ (21)

ここで　 $w(V) = \frac{q^*(V)}{p(V)} \frac{p(V)}{q(V)}$ とすると

　　 $u^*_t = \int_\tau q(V) w(v) v_t dV = \mathbb{E_q}[w(V) v_t ]$ (22)

Importanceサンプリングは(17)式と(14)式を使うと

　　　 $w(V) = \frac{q^*(V)}{p(V)} \exp (\sum_{t=0}^{T-1} - \frac{1}{2} u_t^T \Sigma^{-1}u_t - v_t^T \Sigma^{-1}u_t )$

$w(V) = \frac{1}{\eta} \exp ( - \frac{1}{\lambda} S(V) + \sum_{t=0}^{T-1} - \frac{1}{2} u_t^T \Sigma^{-1}u_t - v_t^T \Sigma^{-1}u_t )$ (23)

　ここで観測で得られた時間毎の誤差 $\varepsilon = (\epsilon_0,\dots,\epsilon_{T-1})$ を使うと $v_t = u_t + \epsilon_t$ なので(23) 式は

　　　 $w(V) =w(\varepsilon)= \frac{1}{\eta} \exp ( - \frac{1}{\lambda} S(U+\varepsilon) + \sum_{t=0}^{T-1} - \frac{1}{2} u_t^T \Sigma^{-1}(u_t+2\epsilon_t))$ (24)

　　　ここで $U=(u_0,\dots,u_{T-1})$ である

　誤差 $\varepsilon$ が分っている場合、(22)の経路の集合 $\tau$ での積分を観測可能な経路の集合に置き換えてサンプリングして、その総和で置き換えると操作 $u_t$ の最適制御は次式で更新できる。

　　　 $u_t^{i+1} = u_t^i + \sum_{n=1}^N w(\varepsilon_n) \epsilon_t^n$

　　　但し $\int_\tau q(V) v_t dV \approx \sum_{n=1}^N \epsilon_t^n$ 　　(26)

(1-5) 状態遷移関数の学習

　コストを最小化（または報酬を最大化）する操作 $u_t$ は(26)式で求められたが、この操作によって状態 $x$ がどの様に推移するかは次のニューロで学習する。

　　　 $x_{t+1} = F(x_t,u_t) = (q_t + \dot{q}_t \Delta t,\dot{q}_t + f(x_t,u_t) \Delta t)$

ここで　

　　　　 $x = (q,\dot{q})$ 状態 $x$ はシステムの状態 $q$ とその変化 $\dot{q}$ とする

　　　　 $f(x_t,u_t)$ は全結合のニューロで、状態 $x_t=(q_t,\dot{q}_t)$ のモニタリングと操作 $u_t$ の記録により学習する。

(2) 実験

　実験は下図の様な砂のトラックの実験場で以下の条件の自動運転で行う。

　まず人間が30分程度毎に様々なスピードで多様な運転を行ってパラメータを取得している。安定的な自動走行が可能になった後、砂上トラックでの自動運転の実験を行っている。

f:id:mabonki0725:20190127181042p:plain — MPPIの実自動車の実験場

　(2-1)実験条件
・誤差 $\varepsilon$

　　　ハンドル： 0.20　スロットル：0.25

　・(6)式のコスト関数　

　　 $q(x) = 2.5(s - s_{des})^2 + 100M(x,y) + 50S_c$

$\phi(x_T) = 100000C$

ここで

　　　 $s$ は走行時のspeed

$s_{des}$ は設定speed

　　　　学習時 9m/s

　　　　試験時 10m/sから13m/sに速度を上げて行う

　　　 $M(x,y)$ はトラック内を格子状にして設定したコスト

　　　　トラックを外れるとコストが大きい

　　　 $S_c$ は横滑り許容角度を超える場合のコスト

　　　　学習時の許容角度は15.76度　試験時の許容角度 21.5度　

　　　 $C$ はクラッシュした場合は１ゴールした場合は0

　(2-2) 実験結果

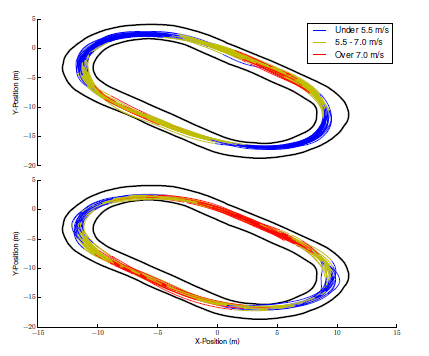
　　訓練は5回行い(45回の周回)、試験はスピードを10m/s から 13m/sに徐々に上げる。下図は上段が訓練時、下段が試験時である。コーナではトラックから逸脱しない様に減速し、直線では増速していることが分る。

f:id:mabonki0725:20190127181808p:plain

(3) 感想

　この論文では制御機能 $v$ と運転操作 $u$ の伝達に多変量正規分布の誤差がある場合で、定められたコストを最小にする強化学習を提案している。

　学習はImportantサンプリングによる最適操作量 $u_t$ と状態遷移 $f(x_t,u_t)$ とで２重に行われている。そのため安定するまで相当な走行が必要と思うが詳細な記述が無い。特に(26)式では観測できる経路の全てについて(24)式のImportantサンプルを求める事が必要である。

　またこのモデルは残念な事に(26)式にある様に全経路と各時点での操作と制御間のエラーの量が予め求められている必要がある。実験ではハンドルとスロットルの誤差のみ設定しているが、本当は各トラック上での操作誤差は事前のトラックの周回中の観測で得ている思われる。本論文のMPPIはパラメータの設定が難しいので、複雑な経路や凹凸がある場所での実機の試験については文献[1]の実績にある様に、短区間のみMPPIを使い、全区間ではメタ学習による更新ロジックと組み合わせるモデルが現実的と思われる。

[1]メタ学習による実世界での変異や誤差に対応した学習の論文を読む - mabonki0725の日記

[2]https://homes.cs.washington.edu/~todorov/papers/TheodorouCDC12.pdf