2018-02-07

FIRLの論文を読むが難しい

AI論文ロボテックス

ベイズによる逆強化学習が、杉山先生の密度比による逆強化学習と同じ手法になったので、残る有名な手法はFIRL(Feature Construction IRL)のみになった。

この手法は下記のAbbeel率いるBarkleyチームのLevineによる論文がある。

https://homes.cs.washington.edu/~zoran/firl.pdf

この手法はこれまでの報酬を固定の特徴量の近似関数で表す手法と全く異なっていて、特徴量を回帰木で分解して有意な特徴量を選択しながら、２次計画法で最適な報酬関数を求める方法となっている。

f:id:mabonki0725:20180207104749p:plain

　　　ここで

　　 $\mathcal{D}$ は熟練者の行動データ

　　　　 $T_{R \to \Phi}$ は回帰木で選択した特徴量

　　　　 $R_{\Phi}$ は改善対象の報酬関数

$||NR_{\Phi}||$ は同じ状態をもつグループを繋ぐ正則化項

　拘束条件では熟練者の行動範囲 $s \in \mathcal{D}$ であれば、正しい価値関数 $V(s)$ が計算され、それを逸脱すると、劣化した価値関数 $V(s)$ が計算される。逸脱した行動 $a$ は観測できないので $\varepsilon$ の罰則を与えている。

　回帰木は、次式で定義され、枝に含まれる状態 $s$ を報酬の寄与で分割して、最適な回帰木は上記の２次計画法で算出している。

　　 $t_j = \{\delta_j,\phi_j,t_{j-},t_{j+}\}$

ここで

　　　 $t_{j-}$ は木の枝でこのノードに含まれる状態 $s$ で報酬に寄与しない側

$t_{j+}$ は木の枝でこのノードに含まれる状態 $s$ で報酬に寄与する側

$\delta(s)$ は状態 $s$ が報酬に寄与するか判断する関数

　　　 $\phi(s)$ は状態 $s$ がこのノードに含まれるかの指標

　 $t_{j-}$ と $t_{j+}$ はさらに回帰木を生成していくが、経験的に浅い分岐でよいとしている。

　この論文は式記号も難しく、本当に妥当な回帰木が得られるか判断が付かない。詳しいロジックを追求するには下記のMatlabのサイトがある。　

github.com

　逆強化学習に詳しい千葉大の荒井研究室ではこのFIRLを昨年稼動して発表している。しかしFIRLの優位性を示せてなく記述も簡単すぎて詳しい事がわからない。　

https://ipsj.ixsq.nii.ac.jp/ej/?action=repository_action_common_download&item_id=162700&item_no=1&attribute_id=1&file_no=1

2018-02-03

ガウス過程による逆強化学習を実装(python)してみる

ロボテックス Python

先日下記の論文について自分の理解を述べたが、文献に沿ったプログラムがあったので、これを自分なりに修正して稼動してみると、完全に自分の理解が誤っていたことが判明した。もし以前の記述を読んだ方がいれば大変申し訳なく、下記にて修正させて頂きます。

Nonlinear Inverse Reinforcement Learning with Gaussian Processes

(1)ロジックの説明

　プログラムによって理解したロジックです。

この手法のプログラムを読むと、ガウス過程の逆強化学習は以下の手順で行っています。

　① 局面を表す特徴量を選定します。

　②熟練者の操作過程の特徴量を記録します。

　⑥の尤度(IRL term)が最大になるまで③から⑥を繰返します。

　　③特徴量の記録から、ガウスカーネル $K_{u,u}$ のパラメータ $\theta$ を最大尤度(GP probability) で計算します

　　 $P(\theta|X_u) = - \frac{1}{2} tr(K^{-2}_{u,u}) - \sum_i \log(\lambda+1)$

　　④次式に従って特徴量 $X_u$ と観測された報酬 $u$ でカーネル過程回帰します

　　 $\log P(u,\theta|X_u) = -\frac{1}{2} u^T K^{-1}_{u,u} u -\frac{1}{2} \log |K_{u,u}| - \frac{n}{2} \log 2\pi + \log P(\theta)$

　⑤擬似報酬 $u$ の事後分布で真の報酬 $r$ を逆算します

　　　この事後分布(GP posterior)は尤度分布と事前分布ともガウス分布なので

　　　理論解で計算できます

　　　 $r = K^T_{r,u} \cdot k^{-1}_{u,u} \cdot u$

　⑥真の報酬 $r$ よりBellman方程式を解いてこの尤度(IRL term)を計算します。

　根拠のロジックは次式の式になります。

f:id:mabonki0725:20180129073901p:plain

　ここで

　　 $D$ は熟練者のデータ

$Xu$ は特徴量

$u$ は観測された報酬

$r$ は真の報酬

　　 $\theta$ はガウス・カーネルのパラメータ

　　IRL termはBellman方程式の解

GP posterior はガウス分布の事後分布

GP probabilityはガウス過程回帰

(2) 実験課題

　５×５のセルにマーク１と２がある。各セルにエージェントは上下左右に移動する

　マーク１からの距離が３以内でかつマーク２からの距離が２以内のセルに居るなら報酬を得る

　マーク１から3超かマーク1に居るなら罰則がある。

　この規則に従うと以下の報酬になる。　

f:id:mabonki0725:20180203095534p:plain

(3) 実装した結果

　　熟練者のデータは上記(2)のルールに従って移動して、その100経路のログを記録している。

　　この行動記録から上記(1)のロジックで報酬を算出している。

　　但し、ARD（Auto Relevant Decision 自動関連決定)のガウスカーネルを使用した。

　　ガウス過程による逆強化学習の結果(右)は真の報酬に近い値となっている。

f:id:mabonki0725:20180203095721p:plain

github.com

参照したプログラムが探しだせなくなったので、自分が修正したプログラムを示します。

2018-01-31

逆強化学習の課題にPlen2を使う

学校の研究でPlen2を使った逆強化学習を企画しているが、初めてPlen2を使ってみた。

このToyロボットはサーボモータでの稼動点が20点あり、ここに信号を送って逆強化学習の実証実験をする。

このPlen2はArdinoが20個のモータを制御する仕掛けで現在8万円弱とまだ高価である。

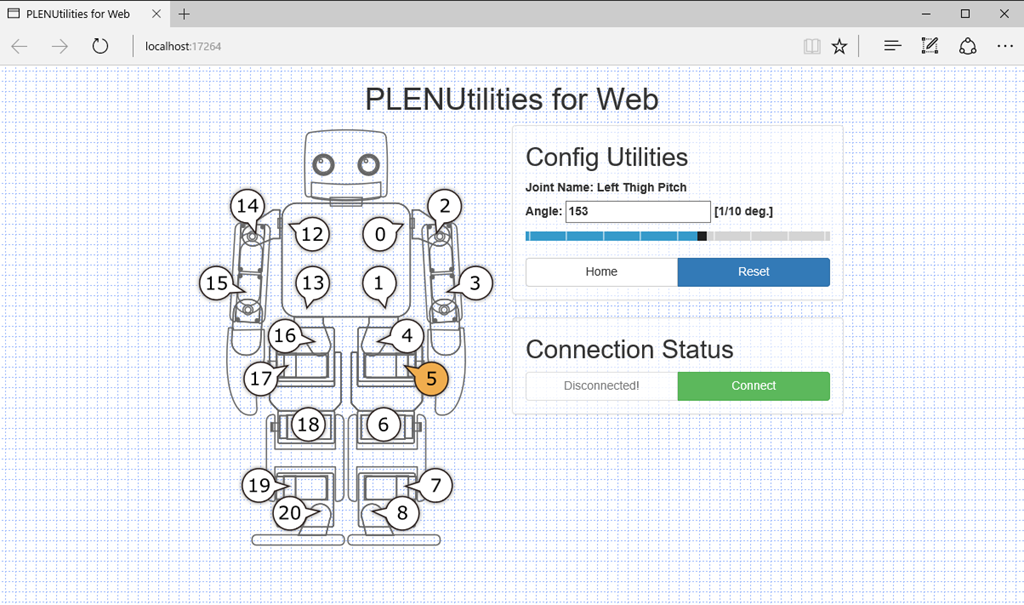
Plen2はPC上のWebを使ったコントロール画面で動作を定義する。

PC上のWebサーバがを通じてPlen2と通信する仕組み。

まずは、下のURLに従ってFirmWareをインストールする。

　http://plen.jp/playground/wiki/tutorials/plen2/firmware

動作に関しては、下図のモーション・編集はExcelのマクロ記憶の様に保存して、これを呼び出す仕掛けだがこの動作にエラーが出ている。

「Plen2 motion」の画像検索結果

2018-01-29

ガウス過程による逆強化学習の論文を読む

最大エントロフィの逆強化学習の性能はベイズより優れていることは実装してみて判明したが、下記の論文によるとガウス過程(Gaussian Process)を使った逆強化学習が傑出してよい性能を出している。　

papers.nips.cc

この論文の高速道路の実験例をみるとパトカーやパトバイクに近い所は人間がスピード抑制をしている事が観測されている。

f:id:mabonki0725:20180129072437p:plain

左上が人間のスピード抑制データ(濃い色）で、GPIRL（ガウス過程逆強化学習）が殆ど等しいことが示されている。ここでの比較先は

　MaxEntIRL(最大エントリフィIRL）

FIRL(Feature Construction IRL)

この手法のプログラムを読むと、ガウス過程の逆強化学習は以下の手順で行っています。

　① 局面を表す特徴量 $X_u$ を選定します。

　②熟練者の操作過程 $\mathcal{D}$ の特徴量を記録します。

　⑥の尤度(IRL term)が最大になるまで③から⑥を繰返します。

　　③特徴量の記録から、ガウスカーネル $K_{u,u}$ のパラメータ $\theta$ を最大尤度(GP probability) で計算します

　　 $P(\theta|X_u) = - \frac{1}{2} tr(K^{-2}_{u,u}) - \sum_i \log(\lambda+1)$

この $\theta$ は特徴量 $X_u$ の正則化項のパラメータです $\theta$ は乱数を振って上式が最大(最尤度)となる値を採用しています。

　　④式(3)に従って特徴量 $X_u$ と観測された報酬 $u$ でカーネル過程回帰します

f:id:mabonki0725:20180129073958p:plain

　　これはカーネル $K_{u,u}$ を分散とする対数分布ですが、最後に $\log P(\theta)$ が追加されています。

　　⑤擬似報酬 $u$ の事後分布で真の報酬 $r$ を逆算します

　　　この事後分布(GP posterior)は尤度分布と事前分布ともガウス分布なので

　　　理論解で計算できます

　　　 $r = K^T_{r,u} \cdot k^{-1}_{u,u} \cdot u$

　　　報酬 $r$ と特徴量 $X_u$ のカーネル $K_{r,u}$ を使っています。問題は報酬 $r$ の算出にこれが未定なのに使っています。よってこの式は仮置きの報酬 $r$ を使って、SGDの繰返しで精緻化する方針としています。

　⑥式(2)の $P(\mathcal{D}|r$ は仮置きの報酬 $r$ よりBellman方程式を解いてこの式(2)尤度(IRL term)を計算します。

f:id:mabonki0725:20180129073901p:plain

　　　ここで

　　　　 $D$ は熟練者のデータ

　　 $Xu$ は特徴量

　　 $u$ はガウス過程

$r$ は報酬

　　　　 $\theta$ は $X_u$ の正則化項

　　　　IRL termはBellman方程式の解

　　GP posterior はガウス分布の事後分布

　　GP probabilityはガウス過程回帰

⑦仮置きの報酬 $r$ をSGDで精緻化するため、本論文ではL-BFGSを使ったと記述があります。この微分式については下記のSupprementに詳細に記述され、Python版ではこの通り実装されています。　　　

Nonlinear Inverse Reinforcement Learning with Gaussian Processes f:id:mabonki0725:20180311155547p:plain

　　SGDの為に以下の微分項を計算する

$\frac{\partial}{\partial \theta} \log P(\mathcal{D},u,\theta|Xu) = \frac{\partial \mathcal{L}_D}{\partial r} \frac{\partial r}{\partial \theta} + \frac{\mathcal{L}_G}{\partial \theta} + \frac{\partial \mathcal{L}_H}{\partial \theta}$

$\frac{\partial}{\partial u} \log P(\mathcal{D},u,\theta|Xu) = \frac{\partial \mathcal{L}_D}{\partial r} \frac{\partial r}{\partial u} + \frac{\partial \mathcal{L}_G}{\partial u}$

ここで諸値は以下で与えられる

　　　 $\frac{\partial\mathcal{L}_D}{\partial r} = \hat{u} - \mathbb{E}(u)$ エネルギーベースの逆強化学習

$\frac{\partial\mathcal{L}_G}{\partial \theta_i} = \frac{1}{2} \mathrm{tr} [\alpha \alpha^T - K_{u,u}^{-1} \frac{\partial K_{u,u}}{\partial \theta_i} ]$ ここで $\alpha = K_{u,u}^{-1} u$

$\frac{\partial\mathcal{L}_G}{\partial \theta_i} = - K_{u,u}^{-1} u$

　　 $\frac{\partial r}{\partial u} = K_{r,u}^T K_{u,u}^{-1}$

$\frac{\partial r}{\partial \theta} = \frac{\partial[r=K_{r,u}^T K_{u,u}^{-1} u]}{\partial \theta_i}$

ここで $\theta = \{\beta,\lambda\}$ なので $\frac{\partial \mathcal{L}_H}{\partial \theta}$ は

　　　 $\frac{\partial \mathcal{L}_H}{\partial \beta} = \mathrm{tr} [K_{u,u}^{-3} \frac{\partial K_{u,u}}{\partial \beta}]$

$\frac{\partial \mathcal{L}_H}{\partial \lambda} = \mathrm{tr} [K_{u,u}^{-3} \frac{\partial K_{u,u}}{\partial \beta} ] - \frac{1}{\sum_i \Lambda_{ii} +1}$

実験課題

黄色の位置から３距離までと赤の位置から２距離の場合に居続けると報酬が加算される（左下の赤い範囲）。コマを上下左右に移動して報酬の多寡で強化学習を行った軌跡をデータとして保存する。

f:id:mabonki0725:20180203095534p:plain

強化学習で学習した軌跡でPythonによるガウス過程を使った逆強化学習の結果が右図。一応左図の真の結果に近く細かい報酬が得られている。

f:id:mabonki0725:20180203095721p:plain

2018-01-24

ベイズによる逆強化学習をＣ言語で実装してみた

　本郷で行われた強化学習アーキテクト(2018/01/16)は千葉大学Dの石川翔太さんのベイズによる逆強化学習であった。

　　https://www.slideshare.net/ShotaIshikawa2/ss-86214928

最大エントロフィ法の逆強化学習を実装して見て納得できなかった事は、熟練者の方策変更を反映できない事であった。

その点ベイズでは熟練者のデータを分類して、その方策の移動を隠れ変数として反映できる可能性がある。

　以下の文献に従って簡単な、ベイズによる強化学習を実装してみた。

　　https://www.aaai.org/Papers/IJCAI/2007/IJCAI07-416.pdf

　プログラム(python) としては下記のGitHubを参照しました。

https://github.com/erensezener/aima-based-irl

　熟練者の選択確率を $P_{expert}(Trj(s,a)|R)$ とすると報酬 $R$ はベイズより次式の事後分布で算出する事ができる。

　　 $P_{expert}(R|Trj(s,a)) = \frac{1}{Z} P_{expert}(Trj(s,a)|R) \cdot P_{expert}(R)$

　　ここで

$s$ :局面

$a$ :行動

$Trj(s,a)$ は観測された熟練者の遷移経路

$P_{expert}(R)$ :熟練者の報酬の事前確率

　　 $Z=\sum_a \gamma \exp \{Q(s,a)|R)\}$ :分配関数

$Q(s,a)|R$ は行動価値関数 Bellman方程式で解く

　隠れ変数Ｒを変動させて事後分布を最大とするMAP(Maximum Posterior)をすればよい

ベイズモデルの有意性は上記の様に定式化が明確で理解し易いことにあるが、一般に事後分布は尤度関数が共役事前分布でないと理論的に解けず、MCMCによる繰返し計算が必要になる。

以下の手順で計算する。

①報酬の事前分布は $R$ 一様分布とする

　②MCMCを使って最適 $R$ を探査する

簡単にいうと一様分布の報酬 $R$ をランダムに変えて生成した熟練者の事後分布が高くなるなら、これを採用する

　③生成する尤度分布 $P(s,a|R)$ は仮定された $R$ よりBellaman方程式を解いて価値行動関数 $Q(s,a|R)$ に指数比例とする(ボルツマン分布の仮定)

　　 $P(R|s,a) = \frac{1}{Z} \exp \{Q(s,a^*)|R)\} \cdot P(R)$

$a^*$ は熟練者の局面 $s$ での最適行動

　　　　この実装では熟練者の経路から局面 $s$ での最頻度行動としている。

　　　　上記のpythonの例だと熟練者の事前報酬 $R^*$ を仮定して採用している。

④ 乱数で生成された報酬 $R$ での熟練者の事後分布が、前に計算された事後分布より高くなれば、この仮定された報酬 $R$ を選択する。

実験課題

　課題は最大エントロフィ逆強化学習と同じ問題とする。

　赤がゴール。熟練者データはOpen-AIで解いた100通りの経路とする。

　　 f:id:mabonki0725:20171215143025p:plain

実験結果

　ゴールに近い所が報酬が高く、遠い所が低く計算できている。

　最大エントロフィ逆強化学習よりは粗い結果となっている。これは熟練者の最適方策を単に経路データから最頻度行動を採用しているためと考えられる。

f:id:mabonki0725:20180124100306p:plain

2018-01-13

UC.Berklayの協業強化学習の論文を読む

複数の自律体での強化学習は敵対的なモデルが一般的ですが、この論文は複数の自律体が協同で問題を達成するモデルの論文で、DeepMindと双璧を成すUC.Berklayの発表です。

https://people.eecs.berkeley.edu/~russell/papers/icml17ws-cirl.

「Efficent Cooperative Inverse Reinforcement Learning」

問題設定はＣhefWorldと云い人間とロボットが協同で料理の材料を用意して、なるべく多くの料理を作るゲームです。

このモデルはAdaptive-CIRLとして以下の実験結果が報告されています。横軸は材料数、縦軸は成功した料理数です。材料数が増えた場合、論文のモデルが傑出して高い精度を出しています。　　 f:id:mabonki0725:20180113115628p:plain

この問題はロボットは人間の意図や好みを推測して材料を提供する必要があるので、ロボット側から見ると人間の好みを観察して合わせる必要があります。それでCIRL(Cooperative Inverse Reinforcement)として人間の行動をデータとする逆強化学習としてモデル化できますが、人間の好みが見えないPOMDP(部分観察マルコフ決定過程）として捉える事ができます。

POMDPでは一般に観察データ $O$ から状況 $s$ を推察する確信度 $b$ を導入します。一般には観察データから正解の状況 $s$ で回帰で求めらることが多いです。

　 $s_k = \theta_{k,1}O_1 + \dots + \theta_{k,n} O_n$

この論文では価値関数 $\alpha_\sigma(s)$ はBellman方程式に類推確率 $P(s,z | s,a)$ を考慮して以下に改変して計算しています。

　 $\alpha_\sigma(s) = R(s) + \gamma \sum_{s' \in S} \sum_{z \in Z} P(s',z | s,a) \alpha_{v(z)} (s')$

　ここで

　　 $z$ ：観察データ

　　 $\alpha_{v(z)}(s')$ は観察zでの状況s'の価値

大きな問題は協業なので、人間の意図に沿わない材料をロボットが用意した場合でも料理にする必要があります。

この論文では、人間の類推確率 $P(s,a^H|s,a^R)$ を以下で更新しています。

　 $P(s',a^H | s,a^R) = P((x',\theta'),a^H | (x,\theta),a^R)))$

$=T(x,a^H,a^R,x')\cdot\mathcal{1}(\theta' = \theta) \cdot P(a^H|x,a^R,\theta)$

ここで

T:推移確率

　　状態 $s$ は(観察 $x$ ,パラメータ $\theta$ )で定義

　　 $a^H$ は人間の行動

　　 $a^R$ はロボットの行動

複数の自律体の強化学習は、逆強化学習よりも互いの意図を確信度で代替するPOMDPでも実現できること示した意義があると考えられます。

2018-01-08

UC.Berkeleyの敵対的逆強化学習の論文を読む

Abbeel率いるUC.Berkeleyのロボット学者達が昨年初「GANとIRL」は同義だとする画期的な論文を示しましたが、この一派がまたこの論文に述べられたGAN-GCLを発展させたGANによるIRLの論文（Adversarial Inverse Reinforcement Learning:AIRL)を発表しました。

[1710.11248] Learning Robust Rewards with Adversarial Inverse Reinforcement Learning

GAN-GCL(Genarative Adversarial Network-Guided Cost Learning)では経路を使った識別関数でしたが、この手法は安定しないため、局面( $s,a$ )での識別関数に変更して性能を向上させました。