2020-10-08

Atariゲームのマルチタスクをネットワークの選別と重ね合わせで実現する論文を読んでみる

David HaのWorldModelsをマルチタスク化できないかと思ってゼミで相談したところ、転移学習の記事の中に下記のネットワークの重ね合わせでマルチタスクを実現した論文を紹介された。

arxiv.org

この論文にはDavid Haも共著として入っているので先進的な強化学習の論文と考えてよさそうである。

この論文の紹介サイトに転移学習とマルチタスクの区別が説明されているが、共に

　既存の知識を使って後継の問題を効率的に解く

は同じである。

転移学習の本来の定義は

　既存の知識の構造を理解し、異なるドメインに適応する手法

しかし最近ではドメインに関わらず後継の問題を効率化する意味に拡大されて混乱する状態になっている。例えば画像診断の事前学習も転移学習とする事に意義を唱えても反論されてしまう。

一方マルチタスクは

　ソースとターゲットを区別せずに、複数のタスクを同時に学習

即ち転移学習は既存知識の援用、マルチタスクはタスク間の共通知識の援用で効率化する違いがあると考えてよさそうである。

・モデル

本論文は２つのゲームを２段階で学習させ、後段ゲームは前段ゲームの知識を利用するのでソースとターゲットが明確な転移学習と考えられる。

本論分は下図の様に深層学習のユニットを連結したもので、即ち深層ネットをさらにネットワーク化したもので、これをPathNetと称している。

本論文では画像識別と強化学習の転移学習の２つの転移学習の実験を行っていいる。下図は強化学習用のPathNetである。画像識別用のPathNetはOutPutが識別ラベルとなる。

f:id:mabonki0725:20201014053501p:plain

PathNetは深層学習のユニットを４層（下流３層はCNN 最上流は密結合)に配置し、１層は10個の深層学習ユニット(8Kernel)で構成されている。層の中間のユニット(水色)は総和ユニットである。

深層学習のConv2Dユニットは複雑なネットワークと思ったが、下記のGitHubで実装した人のプログラムを見る限り(8,4,3)の単純なCNNであった。

github.com

入力はゲーム画面で出力は汎用型強化学習のA3C(並列型ActorCritic）の方策πと価値Vである。上図ではSourceゲームとTargetゲームが上下に配置されるが、順序としてまずSourceゲームがPathNetで学習され、後にTargetゲームが学習される。

強化学習の初期では64人のエージェントが並列にPathNet上をランダムに走り、64人が異なる状態の画面を遷移しながら各CNNも画面の学習を行う。そしてよい報酬が得られたのCNNのルートが残るトーナメント形式になっている。

SourceゲームについてPathNetはゲームの10回エピソードについて最大の報酬が得られるルートを選別し、既存の選別されたルートに重ねあわす事を繰返す。この過程を繰返すことで有意なルートが徐々に収束される。次にTargetゲームが同様な手続きでルート選別され、ルートが重ね合わされる、この場合最初のSourceゲームで収束したルートは常に選別された状態になっている。即ち忘却できない様になっている。この過程を示したのが下図である。

・実験

下図では最初にPongゲームが64人のエージェントでランダムに探索するので、最初の図１では最初はランダムなルートが形成されるが、徐々に図４の水色のルートに収束する。次にTargetのAlienゲームが学習され図9ではルートが収束している。重要な事は最初のゲームのルートは常に選別ルートに残っており、この事がTargetのAlienゲームの初期の学習を容易にしていると思われる。

f:id:mabonki0725:20201007200912p:plain

・考察

　このPathNetの特異な点は、64人のエージェントが独立に走り回ることで、効率のよい画面推移の探索とこの画面認識のCNNの学習が報酬によってトーナメントで評価されながら選別されることである。また一見複雑な仕掛けだが、上記の実装プログラムを見る限り簡潔なプログラムで実装されており優位なモデルと評価できる。転移学習の面でも２番目のゲームの初期効率がいいのは１番目のルートが残っているからと考えられる。しかしこのモデルには忘却がないので、デメリットとして２番目のゲームの学習の障害になっている可能性があり、これが評価できていない。しかし人間のマルチな学習として遺伝的な選択手法で成果を出した点では評価できる。

2020-02-24

Atariゲームの予測画像(worldModel)上で方策改善が効率的であった論文を読んでみる

David HaがVAEで一旦抽象化して生成した擬似動画をWorldModelと称し、このWorldModelの擬似動画での訓練が実画面でも効果があった事を報告している。

夢で学習する強化学習モデルの論文を読む - mabonki0725の日記

今回読んだ論文は複数のAtariゲームでのWorldModel上での訓練が極めて効率的であることを示しており、VAEで一旦抽象化して生成した空間(worldModel)での訓練が一般的に有効なことを示していて大変意義のある論文と思われる。著者等はこのモデルをSimPle(Simulated Policy Learning)と名付けている。

[1903.00374] Model-Based Reinforcement Learning for Atari

今までの強化学習はゲームに依存しないModel-Freeな探索型のモデルであったが、相当学習時間が要する事が知られている。この論文は複数のAtariゲームでも次の図の様にVAEで生成した擬似空間のWorldMode上の訓練と実画面の訓練を繰返すことで、Model-Freeに比べ相当な学習効率がある事を示した。右図の上段は訓練された方策 $\pi$ で操作した実画面での操作推移で、中断では実画面の推移からVAEでWorldModelを生成し、下段はWorldModel上で方策 $\pi$ の改善をしている。左図はこれを再帰的に繰返している事を示している。

f:id:mabonki0725:20200223002143p:plain

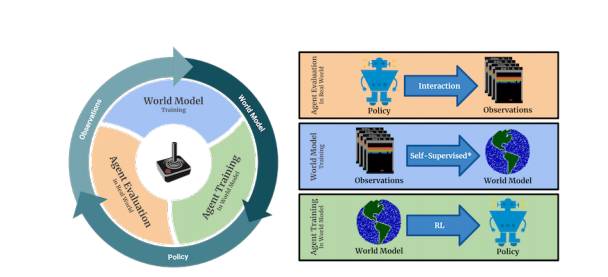
VAEでの強化学習はModel-Baseと称し、次の論文にある様に系列上の潜在変数を収束させ、この潜在空間での訓練する方式であったが、

深層ベイズモデルによる長期予測での強化学習の論文を読む - mabonki0725の日記

動画の状態推移を予測する強化学習の論文を読んでみる - mabonki0725の日記

このModelはDavid HaのWorldModelと同じ生成した擬似空間上での方策 $\pi$ をPPO(Proximal Policy Optimization)で改善しており、表題がModel Baseとあるが、擬似空間上ではModel-Freeであり、Model-BaseとModel-Freeの統合Modelとも云える。

人間の学習には汎化能力があり、一つを習得すると同じ様な課題は容易に可能になる。これは個別の課題に対応しているのではなく、同様な課題の背後にある汎用的な構造を理解し訓練しているからで、即ちこの構造をVAEのencoderが抽象化する潜在空間であり、VAEのDecoderが生成する多様な擬似世界での訓練が現実の多様性での訓練を実現していると考えられる。

・VAEモデル

既にVAEによる強化学習の効率化は周知のことになっているからか、この論文の難易度は高く、下図に示すVAEによる潜在空間を如何に生成するかがアイデアが要旨になっている。

f:id:mabonki0725:20200223003457p:plain

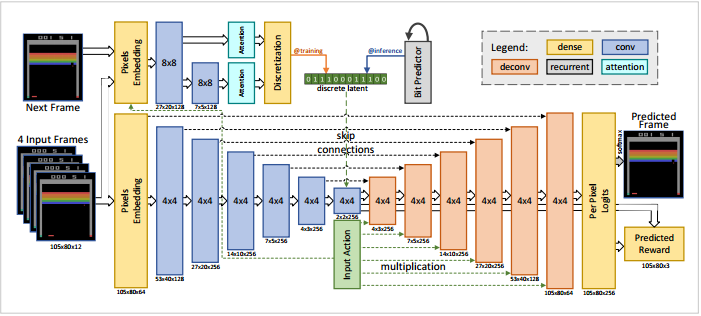
上図に示す様にModelは上下の２段で構成されている。下段は左側からゲームの推移画面（4フレーム）をVAEに入れて中央が潜在空間になっており、右側に予測の次画面と報酬を出力している。また中央に入力画面での操作(行動)をベクトル化して入れている。従ってこのVAEは左側の4実画面と右側の次フレーム画面と実報酬が一致する様に潜在空間を最適化していると考えられる。

上段の左は下段の４フレームの次のフレーム画面を入力としてAttensionで潜在変数を生成しているが、この安定のため上段の左のLSTMより潜在変数の系列に合う様に拘束している。そしてこの潜在変数は下段の中央の潜在空間に反映している。

・方策の改善

方策はPPO(Proximal Policy Optimization)を使っている。これは行動や状態の推移が実数領域でのTRPO(Trust Region Policy Optimization)の改良型であり複数のAgentの報酬を集約して訓練するモデルである。しかしゲームの状態は離散状態しかとり得ないので実領域のPPOは必要ないと思うが、TRPOの提唱者のLavinが著者に入っているので、このPPOのモデルに使い馴れているためかもしれない。PPOは16個の並列のエージェントを使い、訓練は50フレーム毎に行うが、50フレームは訓練には短いので最後のフレームには擬似報酬をPPOで得られた価値 $V$ で与えている。

最上図にある円のサイクルは15回となっていて、WorldModel上の訓練は225ステップが最も良かったと報告している。16個のエージェントによるPPOの繰返しは80万回の数倍で都合1520万回繰返している。

・実験結果

多くのAtariゲームについてModel-Free型の最も学習効率がよいアンサンブル型のRainBowとPPO独自のモデルと比較している。

DeepMindのDQN統合版のRainBowの論文を読む - mabonki0725の日記

DeepMindの多様な環境で順番学習の有用性の論文 - mabonki0725の日記

下図の左がRainbowで右がPPO独自との比較で、各ゲームについて本方法(SimPLe)が10万回（赤線)で得た報酬を得るのに要した比較手法での回数である。単位は10万回

f:id:mabonki0725:20200224220826p:plain

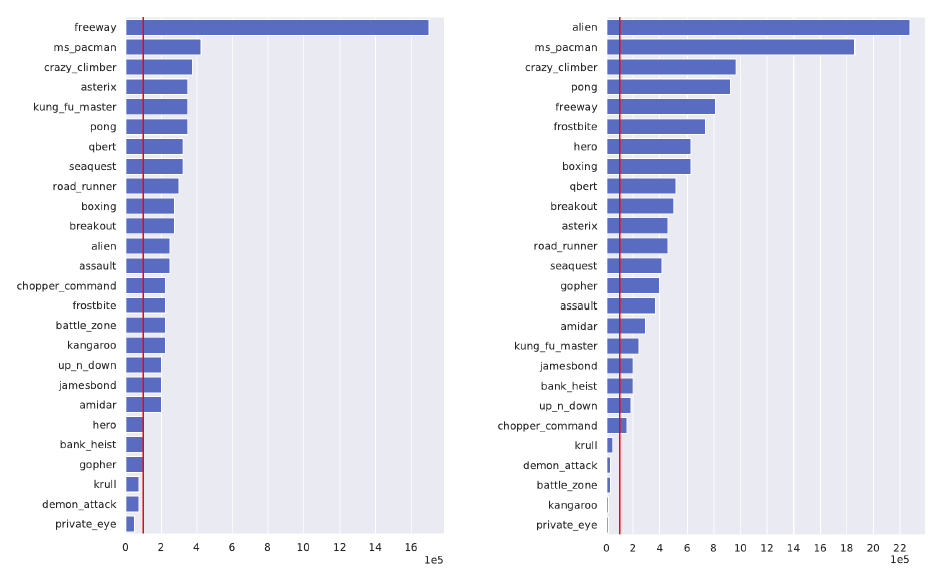
次の表はSimPleで学習サイクルを15回行った報酬(５回の試行の平均）と、RainBow10万回　PPO50万回及び人間の平均スコアとランダムなモデルの比較である。大体RainBow10万回より優れていることが分る。

f:id:mabonki0725:20200224221955p:plain

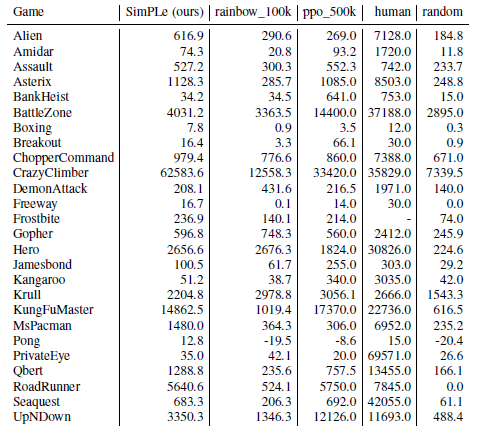
このモデルは実ロボット型のPPOをworldModel上で訓練しているので、実ロボットの視野画面を使ったロボットの学習には有効と考えられる。Lavinも参加しているので次はこの分野の論文が期待される。

2020-02-17

動画の状態推移を予測する強化学習の論文を読んでみる

動画から系列型のVAE方式による状態推移を予測する強化学習として、優秀な学習効率を達成したモデルの論文である。

[1811.04551] Learning Latent Dynamics for Planning from Pixels

系列型VAEの強化学習モデルWorld Modelを最初に発表したDavid Haも著者になっているので、このモデルはWorld Modelの発展型もしれない。

この成果については下記のICMLの口答発表がある。

Learning Latent Dynamics for Planning from Pixels

GitHubにも著者らの実装と動作した動画が揚がっている

GitHub - google-research/planet: Learning Latent Dynamics for Planning from Pixels

この強化学習ではエージェントが一部しか観察 $o_t$ できないPOMDP(Partial Observable Markov Dicision Process)となっていて、次の分布のパラメータ推定をELBO(evidence lower bound)の最大化で推定している。従ってこれらの分布は全て多変量ガウシアンである。

推移モデル $p(s_t|s_{t-1},a_{t-1})$

観察モデル $p(o_t | s_t)$

報酬モデル $p(r_t|s_t)$

Encoder $p(s_t| o_{\leq t},a_{\leq t})$ 　状態 $s_t$ は潜在変数となっている

摂動 $p(\epsilon)$

論文にある全体のアルゴリズムとしては潜在変数の最適化とサンプリングの組合せで以下となっている。

アルゴリズム1

以下を収束まで繰り返す

　　次の潜在変数の最適化を繰り返す

　　　保存された行動軌跡図からバッチ分 $D$ をランダムに取り出す

　　　ELBO(Equation3)で $\mathcal{L}(\theta)$ を解き事後分布の状態潜在変数のパラメータ $\theta$ を求める

　　パラメータを更新する $\theta \leftarrow \theta - \alpha\nabla_\theta\mathcal{L}(\theta)$

サンプリングを繰り返す

　　　状態潜在変数をEncoder $q(s_t|o_{\leq t},a_{\leq t})$ で推定する

　　　推定された状態に行動計画 $planner$ より最適行動を求め、これに摂動を与える

$a_t \leftarrow planner(q(s_t|o_{\leq t},a_{\leq t}),p)$ アルゴリズム2参照

　　　行動をR回繰り返し、

　　　　　報酬 $r_t$ と観察図 $o_t$ を得る。

　　　　繰返した観察図より軌跡図として保存する

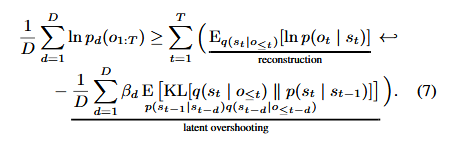
アルゴリズム１中にある $s_t$ の推定の理論は(Equation3)として以下に手案されている。（式の展開は付録8式参照)

左辺の対数尤度を右辺では潜在変数と $s_t$ を介在させて $q(s_t| o_{\leq t},a_{\leq t})$ が一致する様にELBOを解いている。

f:id:mabonki0725:20200217073926p:plain

しかし長い系列のELBOは容易でないので、RNNを採用したRMMSで実装している。

著者らは下図の状態遷移SMMとRNNを合成したRSSM（Recurent State Space Model)を提案している。即ち非線形の状態遷移では誤差が大きく再帰的なRNNの経路を追加して安定化を図っている。ここでSSM（統計的過程）とRNNを（決定的過程）を合成したと言っている。

f:id:mabonki0725:20200216211809p:plain

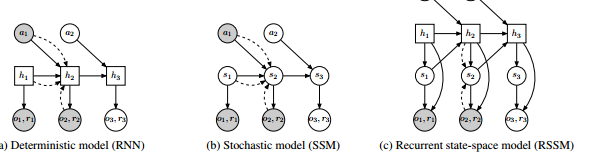
よってRNNの隠れ変数 $h_t$ を使って以下で推定している。

　　 f:id:mabonki0725:20200216211911p:plain

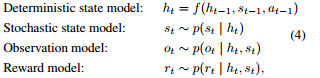
上記を使って便宜的に変分 $q$ を以下に簡略している。

$q(s_t| o_{\leq t},a_{\leq t})=\Pi_{t+1}^T q(s_t|h_t,o_t)$

さらにEquation3での１step毎の推論をｄステップ毎の推論（Latent Overshooting)に拡張している。

f:id:mabonki0725:20200217081424p:plain

下図はlatent Overshootingのd=3の実装図である。左端が１step毎で右端が3step毎の予測となっている。

f:id:mabonki0725:20200217081200p:plain

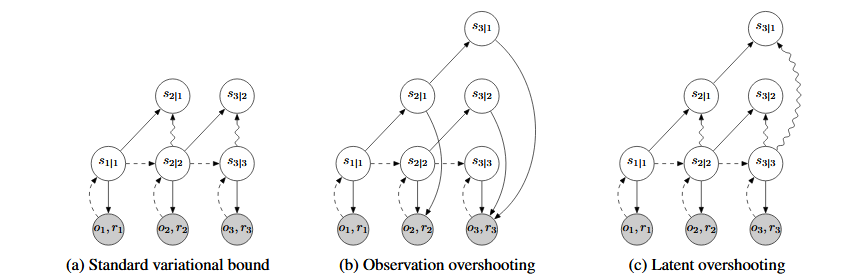
・行動計画 $(planner)$ 行動分布の推定

　探索型の価値関数を使わず今まで良い報酬が得られた行動の分布 $q(a)$ とd-step先の予測から、最適な行動分布を求めている。これについては付録にアルゴリズム２として次の様に記述されているが、要は報酬が良かった行動を集め、このガウス分布を求めているだけである。

　行動軌跡を記録する

良い報酬が得られた行動のガウス分布 $q$ から行動 $a$ をサンプリング

　　　 $a_t \sim q(a_{t:t+H})$

　　d-step先の予測

　　　 $s_{t:t+H+1} \sim q(s_t| o_{\leq t},a_{\leq t}) \Pi _{\tau=t+1}^{t+H+1} p(s_\tau | s_{\tau-1} , a_{\tau-1})$

d-step迄の報酬

$R=\sum_{\tau=t+1}^{t+H+1} \mathbb{E}(p(r_\tau | s_\tau)$

行動軌跡から報酬が高いK個のベストの行動軌跡を取り出す。

ガウス行動推分布 $q(a_{t:t+H})$ の平均と分散を計算する

　　　平均 $\mu_{t:t+H} = \frac{1}{K} \sum_{k \in K} a_{t:t+H}$

分散 $\sigma_{t:t+H} = \frac{1}{K-1} \sum_{k \in K} |a:{t:t+H}-\mu_{t:+H}|$

　　　 $q(a_{t:t+H}) \leftarrow \mathcal{N}(\mu_{t:t+H},\sigma_{t:t+H})$

・実験結果

　実験対象としては行動が実数領域で制御できる下図のDeepMindの６個の課題としている。

f:id:mabonki0725:20200217081841p:plain

実験結果は何れの課題でも200個程度の学習で10万回学習したD4PGのレベルに達しており学習効率が優れていることを示している。

f:id:mabonki0725:20200217082529p:plain

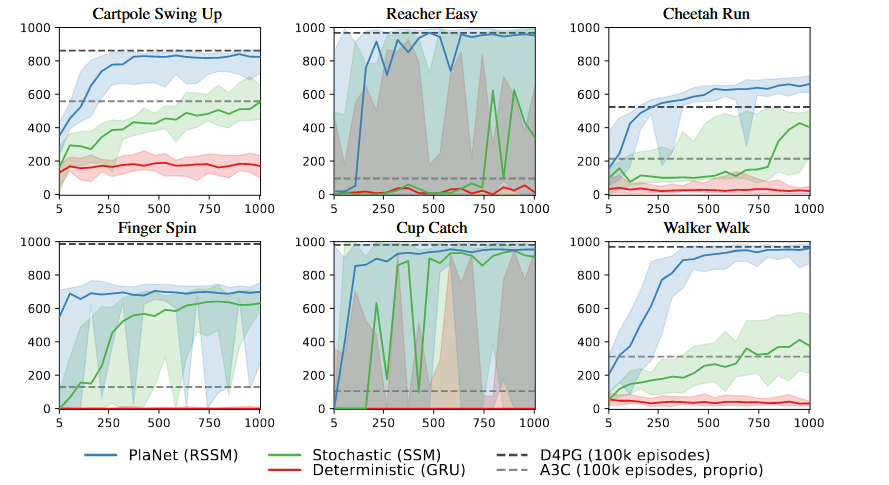
注)DP4Gは実数領域のActor-Critic版のDDPG(Deep Determistic Policy Gradient)を改良したもの

・感想

　このモデルの特質は動画より状況を予測して効率のよい強化学習を達成していることである。

　しかしモデルはVAEのELBOで解く為、潜在変数も行動分布も全てガウシアンになっている。この様な分布が適用できるのは状態推移が一様な課題しか適用できず、ゴールがある様なゲームは容易でないと思われる。しかし実務上の課題は最適な一様状態に達する工夫であり、この様な状態に移行する学習には適用できると考えられる。

　　

2020-02-14

Z-Forcing 再帰深層学習に導入した潜在変数の適合を強いる論文を読む

AI論文自然言語解析

深層生成モデルを使った強化学習が発表されており、この安定化のためZ-Forcingなるモデルを使っていたので、この論文を読んでみる。

深層ベイズモデルによる長期予測での強化学習の論文を読む - mabonki0725の日記

VAEを発展させ再帰深層学習(LSTM)にも潜在変数 $z_t$ を導入して系列での生成モデルを構築する試みがある。このモデルでもVAEと同じ潜在変数を多変量ガウシアンで仮定し、この最適解(平均と分散)は変分ベイズをつかったELBO(Evidence Lower Band)の最大化より求める手法は同じである。しかし長期の系列の潜在変数は適切な収束が難しいのでより学習データに接近させるため、拘束的なZ-Forcingなる手法が提案されている。

[1711.05411] Z-Forcing: Training Stochastic Recurrent Networks

この手法で講演音声の解析や手書き文字の予測、および自然言語の生成を行っていて、特に音声の解析では優秀な結果を出している。

まだ試していないが著者の一人Sordnoniの実装がgithubに揚げている。

GitHub - sordonia/zforcing: ZForcing Repo

生成過程と推定過程を繰返し潜在変数を精緻化するVAEと同様に、次に示す様に再帰的深層生成でも後進時の状態 $b_t$ を使って潜在変数 $z_t$ を精緻化している。

入力 $x_t$ →(生成過程)→潜在変数 $z_t$ ←(推定過程)←状態 $b_t$

しかし系列なので潜在変数が安定的に収束しないため、後進時の状態 $b_t$ と潜在変数 $z_t$ とにガウシアンな強制的関係を補助コストとして導入しようとするのが本論文の手法である。

f:id:mabonki0725:20200213161846p:plain

左図が従来型の潜在変数 $z_t$ を使った系列学習で、右図が本提案のグラフィカル図である。相違としては潜在変数 $z_t$ が推定過程の状態 $b_t$ に依存し、状態 $b_t$ が入力 $x_t$ に拠っていることが分る。青い２重線はその依存関係を示す。

本論では次の様に定式化されている。

・生成過程

　 $h_t = \vec{f}(x_t,h_{t-1},z_t)$

　 $\vec{f}$ は再帰深層学習　

　　 $h_t$ は隠れ変数

・潜在変数の事前分布

$p_\theta(z_t | x_{i:t},z_{1:t}) = \mathcal{N}(z_t:\mu_t^{(p)},\sigma_t^{(p)})$

ここで $[\mu_t^{(p)},\sigma_t^{(p)}] = f^{(p)}(h_{t-1})$

$f^{(p)}$ は対角ガウス分布

・推定(逆)過程

　 $b_t=\overleftarrow{f}(x_{t+1},b_{t+1})$

$q_\phi(z_t | x_t) = \mathcal{N}(z_t:\mu_t^{(q)},\sigma_t^{(q})$

ここで $[\mu_t^{(q)},\sigma_t^{(q)}] = f^{(q)}(h_{t-1},b_t)$

$f^{(q)}$ は深層学習

・補助コスト

　 $q_\xi(b_t | z_t) = \mathcal{N}(z_t:\mu_t^{(a)},\sigma_t^{(a})$

ここで $[\mu_t^{(a)},\sigma_t^{(a)}] = f^{(a)}(z_t)$

$f^{(a)}$ は深層学習

潜在変数 $z_t$ の学習は次の下位限界の最大化となるが、

$\mathcal{L}(x;\theta,\phi,\xi) = \sum_t \mathbb{E}_{q_\phi(z_t|x_t)} [\log p_\theta(x_{t+1}|x_{1:t},z_{1:t}) + \alpha \log p_\xi(b_t|z_t) ] - \mathcal{D}_{KL}(q_\phi(z_t|x_{1:T}) || p_\theta(z_t|x_{1:t},z_{1:t-1}))$

ELBOの定式化するため補助コスト項 $\alpha \log p_\xi(b_t|z_t)$ は期待値から便宜的に外に出し次式で下位限界を最大化する。

$\mathcal{L}(x;\theta,\phi,\xi) = \sum_t \mathbb{E}_{q_\phi(z_t|x_t)} [\log p_\theta(x_{t+1}|x_{1:t},z_{1:t}) ]+ \beta \log p_\xi(b_t|z_t) - \mathcal{D}_{KL}(q_\phi(z_t|x_{1:T}) || p_\theta(z_t|x_{1:t},z_{1:t-1}))$

・実験結果

　(a)スピーチ

　　２つのスピーチの認識実験について最大対数尤度を達成している。

　　 Bizzardは１人の300時間の英語のスピーチ　TIMITは630人による6300個のスピーチである。対数尤度は実測の出現分布と予測分布で求められている。

　　　　 f:id:mabonki0725:20200213220602p:plain

aux:補助コストモデル kla:焼き鈍しKLモデル
　　モデル構成　1024-2048 LSTM 潜在変数の次元256

(b)文字認識

　　再帰方式による手書き文字MNISTの認識で最大の負の対数尤度を達成

　　　　 f:id:mabonki0725:20200213220644p:plain

モデル構成　1024 LSTM

(c)自然言語生成（文章の混合例）

　　自然言語生成の評価としてのPerplexity(正解の確率の逆数:低い方が良い)の比較は示されていない。ここではELBOとIWAE(Important Weight Autoregression)との比較のみ表示している。

f:id:mabonki0725:20200214081026p:plain

本実験は潜在変数による文章の生成をおこなっている。次の映画評価の異なる上下の文章の潜在変数を内挿 $\alpha$ して中間文章の生成をしている。従って最初の例では $\alpha$ に応じて「酷い映画」と「良い映画」との中間の文章を生成している。 $\alpha$ が小さいと上段、大きいと下段に寄る文章を生成している。左は確率の高い言葉のみでの文章で、右はランダムに抽出した文章を生成している。内挿値に従った文章が生成しているのが分かる。

次の例は「暴力」と「楽しい」の間の文章を生成した結果である。

f:id:mabonki0725:20200213221113p:plain

モデル構成はLSTM（500の隠れ変数）言葉は300次元にコード化　潜在変数の次元は64である。

・感想

　GitHubにある実装で試してみなければ評価できないが、長い系列でのAutoEncoderでの潜在変数の解は不安定であると推察される。この論文Z-forcingでは補助コストで入力と潜在変数を拘束して安定化を図っている。しかし文章の様な系列では構造があるのでZ-forcingに頼る必要はないと思われる。この様な手法は非構造的な現象には便利で強化学習での場面の予測には都合がいいかもしれない。

2020-02-10

深層ベイズモデルによる長期予測での強化学習の論文を読む

強化学習画像認識

深層ベイズ（深層生成）モデルは複雑な事象の変化が背後に潜在変数の変動によるものと仮定し、深層ネットワークで最適な潜在変数の変動を解くものである。この論文は潜在変数の変動をデコードして事象を再現し、これを長期予測として強化学習に適用したものである。

[1903.01599] Learning Dynamics Model in Reinforcement Learning by Incorporating the Long Term Future

深層ベイズのVAEは静止画を対象とするが、この論文の課題はAgentが自立的に行動して状況変化する動的場面の予測して強化学習を最適化するものである。

動的なLSTMとVAEを使った強化学習ではDavid HaのWorld Modelがあるが、

夢で学習する強化学習モデルの論文を読む - mabonki0725の日記

このモデルは正則化項やコスト関数を入れ長期の予測を考えたものである。

この論文のモデルでは潜在変数 $z_t$ を使った２つのモデルで構成されている。左図のLSTMと潜在変数を使った行動 $a_t$ と観察 $o_t$ の生成モデル。右図は逆伝播 $b_t$ 変数を使ったd潜在変数 $z_t$ の推定モデルである。

f:id:mabonki0725:20200210142405p:plain

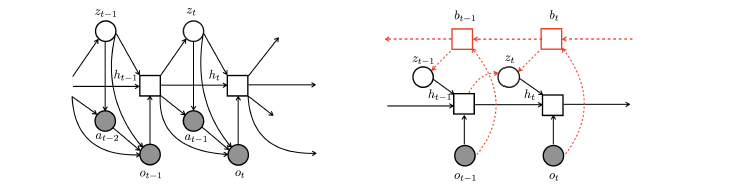
動的な時系列はゲームの熟練者による軌跡から次式のLSTMで学習される。

$h_t =f(o_t,h_{t-1},z_t)$

動的な行動と観察の予測生成モデルは次式のDecoderで逐次的に算出される。

f:id:mabonki0725:20200210143622p:plain

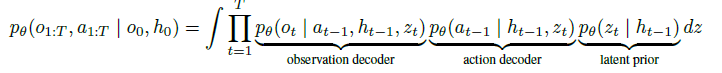
上記のdecoderとpriorは条件付確率でありVAEと同様に正規分布を仮定している。

潜在変数 $z_t$ を安定的にするため、次式のLSTMの逆伝播パラメータ $b_t$ を使った正則化法を入れている。

　　 $b=g(ot,b_{t+1})$

潜在変数 $z_t$ は正則化項をいれた次式のELBO(Evidence Lower Band)を最大化することによって算出される。

f:id:mabonki0725:20200210151157p:plain

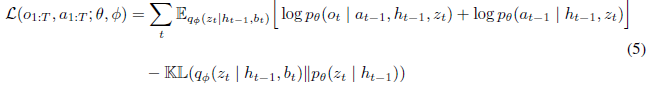
さらに未読だが次式のZ-forcing手法（文献参照)による外部コスト関数を導入して、収束しやすくしている。

f:id:mabonki0725:20200210151741p:plain

[1711.05411] Z-Forcing: Training Stochastic Recurrent Networks

・実験結果１

下記は３つのゲームの試行毎の報酬である。提案手法が最も改善が見られる。論文には図示がないが、CarRacingではこのモデルが道路のコーナを予測再現していることが述べられている。

f:id:mabonki0725:20200210144738p:plain

f:id:mabonki0725:20200210145009p:plain

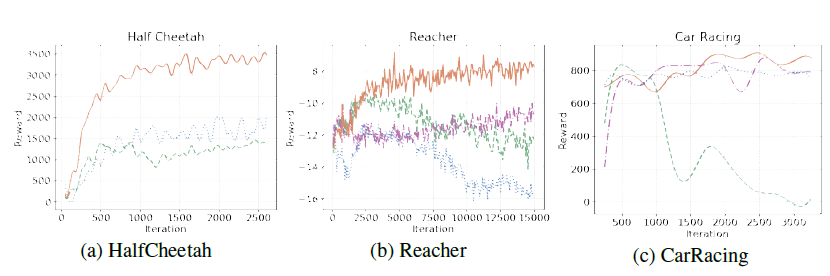
・実験結果２

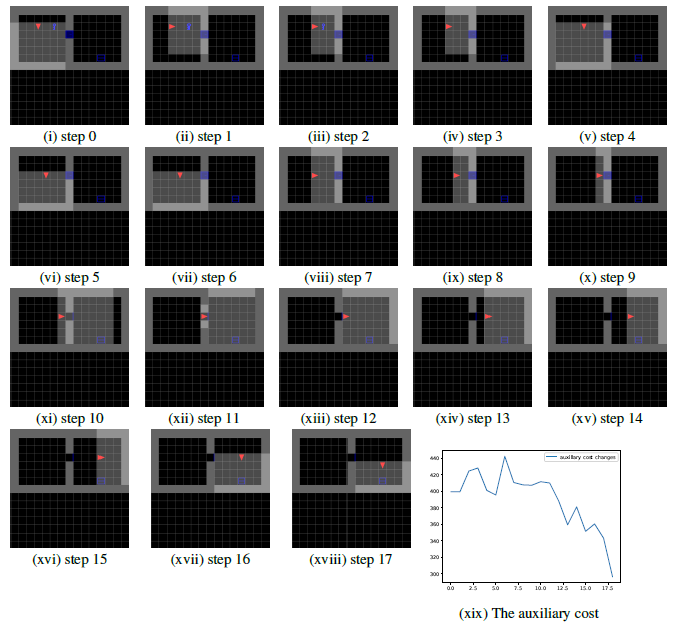
部屋の探索ゲーム(BabyAI)でのサブゴールからゴール検出結果

ゲームの熟練者による1000回の軌跡を学習した後、このモデルが長期予測によってサブゴールが認識できることを示している。

三角がAgentで灰色がAgentの認識領域、青が左右の部屋のドアで右部屋の薄い青がゴールである。

下図の推移からサブゴールである青いドアを認識してゴールに至っていることが分かる。

また最下の折れ線は推移毎のゴールに至るコスト値であり、サブゴール探索には高いコストを費やしており通りすぎると急激に低減していることが分かる。

f:id:mabonki0725:20200210145235p:plain

・感想

　VAEに代表される潜在変数の空間で一旦抽象化してモデル化する手法は人間の様々な具象を抽象化する能力に似ているとされている。これを使ったものとしてDavid Haの世界モデルやDeepMindの２Dから３Dを推定するGQNがある。この流れはVAEをかなり複雑な動的な事象にも適用しようとするもので、実装が極端に難しくなっている気がする。理論も実装も相当実力が要る時期になってきた。

2020-02-06

室内画面の生成する階層型VAEの論文を読む

系列環境での強化学習を考えるため、まず環境を生成するモデルとして下記を読んでみる。

この論文は室内画面を多数生成するモデルで階層型のVAEを使っている。

[1807.09193] GRAINS: Generative Recursive Autoencoders for INdoor Scenes

f:id:mabonki0725:20200206142128p:plain

階層型のVAEはSocherが自然言語で2011年に既に発表していてこの日記にも書いている

Socherの本格的な意味解析の論文 - mabonki0725の日記

Socherはこの階層型を画像の認識でも適用して３D物体の分解も試みている

https://papers.nips.cc/paper/4773-convolutional-recursive-deep-learning-for-3d-object-classification.pdf

この論文は多数の室内の写真について以下の手続きで階層を学習させている

①写真のラベル付け（これは画像識別のモデルを使っている

②壁の近い方から物体の位置関係を階層木で構成している。これは一種の構文解析となっている

　root → 壁１→ソファ→クッション

　　　　　　　　　　→植木

　　　　壁2→ベッド→右ランプ

→左ランプ

③この階層には位置関係と相対距離が入っている

f:id:mabonki0725:20200206145008p:plain

④階層のノードと相対位置および階層関係をベクトル化する

⑤上記のベクトルをVAEで潜在変数にエンコードする

　VAEの潜在変数は全て多変量正規分布とする

⑥潜在変数をデコードして階層を復元する

⑦　⑤と⑥が一致する様に潜在変数を最適化する

f:id:mabonki0725:20200206150509p:plain

⑧最適化された潜在変数をランダムに抽出して様々な階層木を作成し

　階層ノード毎の画像により２Dの室内図を生成する

f:id:mabonki0725:20200206150638p:plain

⑨２Dの室内図より３Dの画像を生成する

f:id:mabonki0725:20200206152342p:plain

この論文の特徴としては

①階層ノードをベクトル化したこれをVAEで近似していて、画像をVAEで学習しているのではない

②階層木の各ノードの位置関係より室内図を再現している。

2019-04-25

微細な手型実機ロボットでの強化学習の論文を読む

実機ロボットとしては歩行型ロボットや自律型操作ロボット(PR2)[1]があるが、今回の論文のロボットは微細な操作ができる手形のロボットの強化学習である。

[1808.00177] Learning Dexterous In-Hand Manipulation

　　　　　　 f:id:mabonki0725:20190425124105p:plain

この手形ロボットでは微細な操作で下図の様に立方体や角柱を回させて目的の面(E)を出す一連の動作で、物体を落とすことがなく連続して早く回転させる事を目指している。

f:id:mabonki0725:20190423073245p:plain

上図では各指にモーションキャプチャーを装着していおり、さらに中央のロボットの回りに状態監視のため16個のカメラと3個の高画質カメラを配置した下図の様な大型の装置になっている。

f:id:mabonki0725:20190425121817p:plain

この手形ロボットは「Shadow Dexterous Hand」の名称で人間の手と同じ操作ができる様に2005年に製造され販売されているが、余りにも制御が複雑で普及されていない。

本論文の目的は計算機上の手型ロボットのシュミレータで十分に強化学習の訓練を行い、この結果で実機の手型ロボットで目的の操作を試してみる事である。

シュミレータで訓練し実機で試す方法の長所と短所は以下である。

(A) シュミレータで訓練を行う長所

　1)実機では行えない程の訓練を繰返すことが可能である。

　2)特にLSTMを使った記憶型の強化学習モデルでは相当な学習データが必要になる。

(B)一方シュミレータの短所は以下である。

　1)計算機上の訓練成果は摩擦やモータ誤差や重力が無く、訓練成果が実機で適応できるか不明である。

　2)この「Shadow Dexlerous Hand」では接触や圧力を感知するセンサーが付いているがシュミレーションではこのデータが生かせない。

本論文では短所の1)に対して、シュミレーション上で様々な摂動を与えて訓練することで、学習には時間が懸かるが現実でのギャップを対処しようとしている。しかし短所の2)の触覚データの無視して観察だけでの学習は、人間が鉛筆やハンドル操作の学習の殆どに触覚に頼っている事を考えると、本論文での学習は致命的な欠陥を有していることが分る。

シュミレータでは意図した訓練が繰返しできるが、このシュミレータには触覚や嗅覚の様なセンサー情報が反映できず、意図した以外の訓練も不可能である。

(1)手法

この手型の学習は、実機での転移を考慮して摂動を与えたシュミレータ上で以下の強化学習を採用している。

実機で様々な影響を考えた訓練は数年かかるが、この摂動を入れるシュミレーションによって数時間で訓練できるとしている。

　　 f:id:mabonki0725:20190425132638p:plain